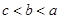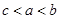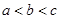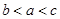题目内容
设二次函数f(x)=(k-4)x2+kx
,对任意实数x,有f(x)≤6x+2恒成立;数列{an}满足an+1=f(an).
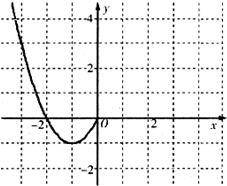
(1)求函数f(x)的解析式和值域;
(2)证明:当an∈(0,
)时,数列{an}在该区间上是递增数列;
(3)已知a1=
,是否存在非零整数λ,使得对任意n∈N*,都有log3(
)+log3(
)+…+log3(
)>-1+(-1)n-12λ+nlog32恒成立,若存在,求之;若不存在,说明理由.
|
(1)求函数f(x)的解析式和值域;
(2)证明:当an∈(0,
| 1 |
| 2 |
(3)已知a1=
| 1 |
| 3 |
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
(1)由f(x)≤6x+2恒成立,等价于(k-4)x2+(k-6)x-2≤0恒成立,
从而得:
,化简得
,从而得k=2,所以f(x)=-2x2+2x,
其值域为(-∞,
].
(2)an+1-an=f(an)-an=-2
+2an-an=-2(an-
)2+
,an∈(0,
)⇒-
<an-
<
⇒(an-
)2<
⇒-2(an-
)2>-
⇒-2(an-
)2+
>0,
从而得an+1-an>0,即an+1>an,所以数列{an}在区间(0,
)上是递增数列.
(3)由(2)知an∈(0,
),
从而
-an∈(0,
),
-an+1=
-(-2
+2an)=2
-2an+
=2(an-
)2,
即
-an+1=2(
-an)2.
令bn=
-an,则有bn+1=2
且bn∈(0,
);
从而有lgbn+1=2lgbn+lg2,可得lgbn+1+lg2=2(lgbn+lg2),
∴数列{lgbn+lg2}是lgb1+lg2=lg
为首项,公比为2的等比数列,
从而得lgbn+lg2=lg
•2n-1=lg(
)2n-1,
即lgbn=lg
,
∴bn=
=
(
)2n-1,
∴
=
=2•32n-1,
∴log3(
)=log3(2•32n-1)=log32+2n-1,
∴,log3(
)+log3(
)+…+log3(
)=nlog32+
=2n+nlog32-1.
即2n+nlog32-1>(-1)n-12λ+nlog32-1,所以,2n-1>(-1)n-1λ恒成立.
(1)当n为奇数时,即λ<2n-1恒成立,当且仅当n=1时,2n-1有最小值1为.∴λ<1.
(2)当n为偶数时,即λ>-2n-1恒成立,当且仅当n=2时,有最大值-2为,∴λ>-2.
∴对任意n∈N*,有-2<λ<1,又λ非零整数,∴λ=-1.
从而得:
|
|
其值域为(-∞,
| 1 |
| 2 |
(2)an+1-an=f(an)-an=-2
| a | 2n |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 16 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 4 |
| 1 |
| 8 |
从而得an+1-an>0,即an+1>an,所以数列{an}在区间(0,
| 1 |
| 2 |
(3)由(2)知an∈(0,
| 1 |
| 2 |
从而
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| a | 2n |
| a | 2n |
| 1 |
| 2 |
| 1 |
| 2 |
即
| 1 |
| 2 |
| 1 |
| 2 |
令bn=
| 1 |
| 2 |
| b | 2n |
| 1 |
| 2 |
从而有lgbn+1=2lgbn+lg2,可得lgbn+1+lg2=2(lgbn+lg2),
∴数列{lgbn+lg2}是lgb1+lg2=lg
| 1 |
| 3 |
从而得lgbn+lg2=lg
| 1 |
| 3 |
| 1 |
| 3 |
即lgbn=lg
(
| ||
| 2 |
∴bn=
(
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
∴
| 1 | ||
|
| 1 |
| bn |
∴log3(
| 1 | ||
|
∴,log3(
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1-2n |
| 1-2 |
即2n+nlog32-1>(-1)n-12λ+nlog32-1,所以,2n-1>(-1)n-1λ恒成立.
(1)当n为奇数时,即λ<2n-1恒成立,当且仅当n=1时,2n-1有最小值1为.∴λ<1.
(2)当n为偶数时,即λ>-2n-1恒成立,当且仅当n=2时,有最大值-2为,∴λ>-2.
∴对任意n∈N*,有-2<λ<1,又λ非零整数,∴λ=-1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
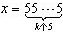 时,都有f(x)=
时,都有f(x)=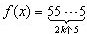 成立?请给出结论,并加以证明.
成立?请给出结论,并加以证明.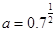 ,
,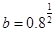 ,
,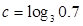 ,则
,则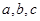 之间的大小关系是( )
之间的大小关系是( )