题目内容
已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.
(1)现已画出函数f(x)在y轴左侧的图象,如图所示,请补出完整函数f(x)的图象,并根据图象写出函数f(x)的增区间;
(2)写出函数f(x)的解析式和值域.
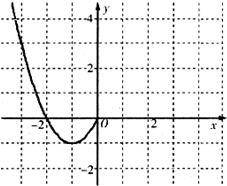
(1)现已画出函数f(x)在y轴左侧的图象,如图所示,请补出完整函数f(x)的图象,并根据图象写出函数f(x)的增区间;
(2)写出函数f(x)的解析式和值域.

(1)因为函数为偶函数,故图象关于y轴对称,补出完整函数图象如有图:
所以f(x)的递增区间是(-1,0),(1,+∞).
(2)设x>0,则-x<0,所以f(-x)=x2-2x,因为f(x)是定义在R上的偶函数,所以f(-x)=f(x),所以x>0时,f(x)=x2-2x,
故f(x)的解析式为f(x)=
值域为{y|y≥-1}

所以f(x)的递增区间是(-1,0),(1,+∞).
(2)设x>0,则-x<0,所以f(-x)=x2-2x,因为f(x)是定义在R上的偶函数,所以f(-x)=f(x),所以x>0时,f(x)=x2-2x,
故f(x)的解析式为f(x)=
|
值域为{y|y≥-1}


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
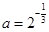 ,
,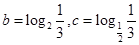 ,则( )
,则( )