题目内容
5.若四面体ABCD的棱长都相等,则AB与平面BCD所成角的余弦值等于( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
分析 在四面体ABCD中,过A作AH⊥平面BCD于点H,则H为底面正三角形BCD的重心,连接BH,则∠ABH=α,就是AB在平面BCD所成角,解直角三角形ABH即可.
解答  解:如图:在等边三角形BCD中,BM为CD边上的高,再在四面体ABCD中,过A作AH⊥平面BCD于点H,则H为底面正三角形BCD的重心,则∠ABH=α,就是AB在平面BCD所成角,
解:如图:在等边三角形BCD中,BM为CD边上的高,再在四面体ABCD中,过A作AH⊥平面BCD于点H,则H为底面正三角形BCD的重心,则∠ABH=α,就是AB在平面BCD所成角,
设棱长为a,由BM为CD边上的高,
则BM=$\frac{\sqrt{3}}{2}a$,在Rt△ABH中,则BH=$\frac{2}{3}$BM
=a$•\frac{\sqrt{3}}{2}×\frac{2}{3}=\frac{\sqrt{3}}{3}a$,
∴cosα=$\frac{BH}{AB}=\frac{\frac{\sqrt{3}}{3}a}{a}=\frac{\sqrt{3}}{3}$.
故选:D.
点评 本题考查了直线与平面所成的角,关键是找到斜线在平面内的射影,把空间角转化为平面角求解.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
10.对于任意两个自然数m,n,定义某种?运算如下:当m,n都为奇数或偶数时,m?n=m+n;当m,n中一个为偶数,另一个为奇数时,m?n=mn.则在此定义下,集合M={(a,b)|a?b=18,a∈N,b∈N}中的元素个数为( )
| A. | 26 | B. | 25 | C. | 24 | D. | 23 |
17.已知函数f(x+1)是定义在R上的奇函数,若对于任意给定的不等实数x1,x2,不等式(x1-x2)[f(x1)-f(x2)]>0恒成立,则不等式f(1-x)<0的解集为( )
| A. | (1,+∞) | B. | (0,+∞) | C. | (-∞,0) | D. | (-∞,1) |
16.已知Sn是等差数列{an}的前n项和,若a2015=S2015=2015,则首项a1=( )
| A. | 2015 | B. | -2015 | C. | 2013 | D. | -2013 |
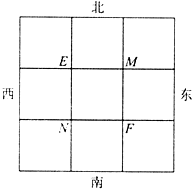 已知甲、乙两人分别位于图中的M、N两点,每隔1分钟,甲、乙两人分别向东南西北四个方向的其中一个方向行走1格,且甲向四个方向行走的概率是相等的,乙向东、向西行走的概率都是$\frac{1}{3}$,向北行走的概率是$\frac{1}{4}$,甲、乙分别向某个方向行走的事件记为A、B.
已知甲、乙两人分别位于图中的M、N两点,每隔1分钟,甲、乙两人分别向东南西北四个方向的其中一个方向行走1格,且甲向四个方向行走的概率是相等的,乙向东、向西行走的概率都是$\frac{1}{3}$,向北行走的概率是$\frac{1}{4}$,甲、乙分别向某个方向行走的事件记为A、B. 如图,是某市1000户居民月平均用电量的频率分布直方图,
如图,是某市1000户居民月平均用电量的频率分布直方图,