题目内容
4.若函数f(x)的单调增区间是[-1,2],单调减区间是[2,3],则f($\frac{2x}{x+2}$)的单调增区间是[-1,2].分析 确定y=$\frac{2x}{x+2}$=2-$\frac{4}{x+2}$在(-2,+∞)上是增函数,利用函数f(x)的单调增区间是[-1,2],可得结论.
解答 解:y=$\frac{2x}{x+2}$=2-$\frac{4}{x+2}$在(-2,+∞)上是增函数,
∵函数f(x)的单调增区间是[-1,2],
∴函数f($\frac{2x}{x+2}$)的单调增区间是[-1,2],
故答案为:[-1,2].
点评 本题考查函数的单调性,考查学生分析解决问题的能力,比较基础.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
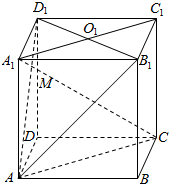 如图,O1是正方体ABCD-A1B1C1D1的面A1B1C1D1的中心,M是对角线A1C和截面B1D1A的交点,求证:O1、M、A三点共线.
如图,O1是正方体ABCD-A1B1C1D1的面A1B1C1D1的中心,M是对角线A1C和截面B1D1A的交点,求证:O1、M、A三点共线.