题目内容
8．
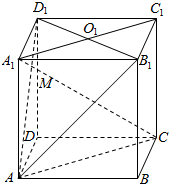如图，O1是正方体ABCD-A1B1C1D1的面A1B1C1D1的中心，M是对角线A1C和截面B1D1A的交点，求证：O1、M、A三点共线．
分析 由已知条件推导出O1、M、A是平面AC1和平面AB1D1的公共点，由此利用公理三能证明O1、M、A三点共线．
解答 证明：∵O1是正方体ABCD-A1B1C1D1的面A1B1C1D1的中心，
∴A1C1∩B1D1=O1，∴O1∈A1C1，且O1∈B1D1，
∵A1C1?平面AC1，B1D1?平面AB1D1，
∴O1∈平面AC1，且O1∈平面AB1D1，
∵M是对角线A1C和截面B1D1A的交点，
∴M∈A1C，且M∈截面B1D1A，
∵A1C?平面AC1，
∴M∈平面AC1，且M∈平面AB1D1，
∵A∈平面AC1，且A∈平面AB1D1，
∴O1、M、A是平面AC1和平面AB1D1的公共点，
∴O1、M、A三点共线．
点评 本题考查三点共线的证明，是基础题，解题时要认真审题，合理运用公理三，注意空间思维能力的培养．
练习册系列答案
相关题目
3．若方程x2sinα-y2cosα=1（0≤α＜2π）表示焦点在x轴上的椭圆，则α的取值范围是（ ）
| A． | （$\frac{3}{4}$π，π） | B． | （$\frac{π}{4}$，$\frac{3}{4}$π） | C． | （$\frac{π}{2}$，π） | D． | （$\frac{π}{2}$，$\frac{3}{4}$π） |