题目内容
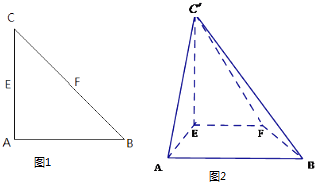
【题目】如图，在△ABC中，∠ABC＝90°，AB＝
，BC＝1，P为△ABC内一点，∠BPC＝90°.
(1)若PB＝
，求PA；
(2)若∠APB＝150°，求tan∠PBA.
【答案】（1）
（2）
【解析】试题分析:（1）在三角形中，两边和一角知道，该三角形是确定的，其解是唯一的，利用余弦定理求第三边.（2）利用同角三角函数的基本关系求角的正切值.（3）若是已知两边和一边的对角，该三角形具有不唯一性，通常根据大边对大角进行判断.（4）在三角兴中，注意
这个隐含条件的使用.
试题解析:解：（1）由已知得∠PBC＝60°，所以∠PBA＝30°.
在△PBA中，由余弦定理得PA2＝
.
故PA＝
. 5分
（2）设∠PBA＝α，由已知得PB＝sin α.
在△PBA中，由正弦定理得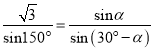
，
化简得
cos α＝4sin α.
所以tan α＝
，即tan∠PBA＝
. 12分
【题目】假设关于某种设备的使用年限
(年)与所支出的维修费用
(万元)有如下统计资料：
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
已知
， 
.
， 
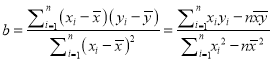(1)求
， 
；
(2) 
与
具有线性相关关系，求出线性回归方程；
(3)估计使用年限为10年时，维修费用约是多少？
【题目】电视连续剧《人民的名义》自2017年3月28日在湖南卫视开播以来，引发各方关注，收视率、点击率均占据各大排行榜首位．我们用简单随机抽样的方法对这部电视剧的观看情况进行抽样调查，共调查了600人，得到结果如下：其中图1是非常喜欢《人民的名义》这部电视剧的观众年龄的频率分布直方图；表1是不同年龄段的观众选择不同观看方式的人数．
表1
观看方式 | 电视 | 网络 |
| 150 | 250 |
| 120 | 80 |
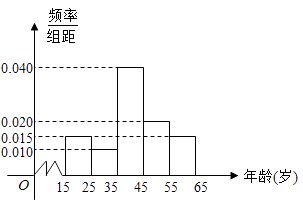
求：（I）假设同一组中的每个数据用该组区间的中点值代替，求非常喜欢《人民的名义》这部电视剧的观众的平均年龄；
（II）根据表1，通过计算说明我们是否有99%的把握认为观看该剧的方式与年龄有关？
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附： 
