题目内容
【题目】已知椭圆C的两个顶点分别为A(﹣2,0),B(2,0),焦点在x轴上,离心率为 ![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)点D为x轴上一点,过D作x轴的垂线交椭圆C于不同的两点M,N,过D作AM的垂线交BN于点E.求证:△BDE与△BDN的面积之比为4:5.
【答案】解:(Ⅰ)由椭圆的焦点在x轴上,设椭圆方程: ![]() (a>b>0),
(a>b>0),
则a=2,e= ![]() =
= ![]() ,则c=
,则c= ![]() ,
,
b2=a2﹣c2=1,
∴椭圆C的方程 ![]() ;
;
(Ⅱ)证明:设D(x0 , 0),(﹣2<x0<2),M(x0 , y0),N(x0 , ﹣y0),y0>0,
由M,N在椭圆上,则 ![]() ,则x02=4﹣4y02 ,
,则x02=4﹣4y02 ,
则直线AM的斜率kAM= ![]() =
= ![]() ,直线DE的斜率kDE=﹣
,直线DE的斜率kDE=﹣ ![]() ,
,
直线DE的方程:y=﹣ ![]() (x﹣x0),
(x﹣x0),
直线BN的斜率kBN= ![]() ,直线BN的方程y=
,直线BN的方程y= ![]() (x﹣2),
(x﹣2),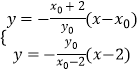 ,解得:
,解得: 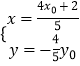 ,
,
过E做EH⊥x轴,△BHE∽△BDN,
则丨EH丨= ![]() ,
,
则 ![]() =
= ![]() ,
,
∴:△BDE与△BDN的面积之比为4:5.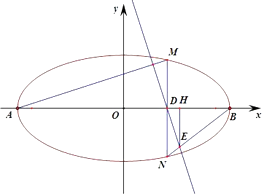
【解析】(Ⅰ)由题意设椭圆方程,由a=2,根据椭圆的离心率公式,即可求得c,则b2=a2﹣c2=1,即可求得椭圆的方程;
(Ⅱ)由题意分别求得DE和BN的斜率及方程,联立即可求得E点坐标,根据三角形的相似关系,即可求得 ![]() =
= ![]() ,因此可得△BDE与△BDN的面积之比为4:5.
,因此可得△BDE与△BDN的面积之比为4:5.
【考点精析】利用点斜式方程和椭圆的标准方程对题目进行判断即可得到答案,需要熟知直线的点斜式方程:直线![]() 经过点
经过点![]() ,且斜率为
,且斜率为![]() 则:
则:![]() ;椭圆标准方程焦点在x轴:
;椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目