题目内容

【题目】如图所示，在正方体ABCD-A1B1C1D中，S是B1D1的中点，E、F、G分别是BC、CD和SC的中点．求证：

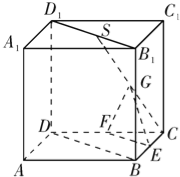
（1）直线EG∥平面BDD1B1；

（2）平面EFG∥平面BDD1B1．

【答案】详见解析

【解析】

试题分析：（1）要证明线面平行，可先证明线线平行，所以连接,根据三角形中位线，可证明得到,这样问题就迎刃而解了；（2）要证明面面平行，可先证明平面内的两条相交直线平行与另一个平面内的两条相交直线，将问题转化为证明两组线线平行，,,或是,这样问题得证.

试题解析：（1）连结SB，由已知得EG∥SB，由此能证明直线EG∥平面BDD1B1．

（2）连结SD，由已知得FG∥SD，

从而FG∥平面BDD1B1，

又直线EG∥平面BDD1B1，

（2）由此能证明平面EFG∥平面BDD1B1．

练习册系列答案
相关题目

【题目】若定义在上的函数满足，且是奇函数，现给出下列4个结论：①是周期为4的周期函数；

②的图象关于点对称；

③是偶函数；

④的图象经过点,其中正确结论的序号是__________（请填上所有正确的序号）．

【题目】在平面直角坐标系xOy中，已知椭圆C： =1（a＞b＞0）的离心率为 ，椭圆C截直线y=1所得线段的长度为2 ．

（Ⅰ）求椭圆C的方程；
（Ⅱ）动直线l：y=kx+m（m≠0）交椭圆C于A，B两点，交y轴于点M．点N是M关于O的对称点，⊙N的半径为|NO|．设D为AB的中点，DE，DF与⊙N分别相切于点E，F，求∠EDF的最小值．

【题目】已知椭圆C的两个顶点分别为A（﹣2，0），B（2，0），焦点在x轴上，离心率为 ．
（Ⅰ）求椭圆C的方程；
（Ⅱ）点D为x轴上一点，过D作x轴的垂线交椭圆C于不同的两点M，N，过D作AM的垂线交BN于点E．求证：△BDE与△BDN的面积之比为4：5．

【题目】某公司计划2011年在甲、乙两个电视台做总时间不超过300分钟的广告，广告费用不超过9万元.甲、乙电视台的广告收费标准分别为500元/分钟和200元/分钟.假定甲、乙两个电视台为该公司每分钟所做的广告，能给公司带来的收益分别为0.3 万元和0.2万元.问：该公司如何分配在甲、乙两个电视台的广告时间，才能使公司收益最大，最大收益是多少万元？

【题目】在(2x-3y)10的展开式中,求:

(1)各项的二项式系数的和;

(2)奇数项的二项式系数的和与偶数项的二项式系数的和;

(3)各项系数之和;

(4)奇数项系数的和与偶数项系数的和.

【题目】如图，在三棱锥中，分别是的中点，

（1） 求证：平面；

（2） 求异面直线与所成角的余弦值；

（3） 求点到平面的距离。

【题目】为了研究一种新药的疗效，选100名患者随机分成两组，每组各50名，一组服药，另一组不服药．一段时间后，记录了两组患者的生理指标x和y的数据，并制成如图，其中“*”表示服药者，“+”表示未服药者．（13分）
（1）从服药的50名患者中随机选出一人，求此人指标y的值小于60的概率；
（2）从图中A，B，C，D四人中随机选出两人，记ξ为选出的两人中指标x的值大于1.7的人数，求ξ的分布列和数学期望E（ξ）；
（3）试判断这100名患者中服药者指标y数据的方差与未服药者指标y数据的方差的大小．（只需写出结论）

【题目】如图，四棱锥P﹣ABCD中，侧面PAD为等边三角形且垂直于底面ABCD，AB=BC= AD，∠BAD=∠ABC=90°． （Ⅰ）证明：直线BC∥平面PAD；
（Ⅱ）若△PAD面积为2 ，求四棱锥P﹣ABCD的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网