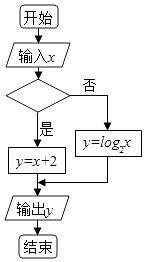
题目内容
【题目】如图,在四棱锥A-BCDE中,底面BCDE是等腰梯形,BC∥ DE,∠ DCB=45°,O是BC中点,AO=![]() ,且BC=6,AD=AE=2CD=
,且BC=6,AD=AE=2CD=![]() .
.
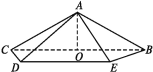
(1)证明:AO⊥平面BCD;
(2)求二面角A-CD-B的平面角的正切值.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接OD。在三角形OCD中,利用余弦定理求出OD,在三角形AOD中通过验证勾股定理可得AD⊥ OD.同理可得AO⊥OE。故可得出AO⊥ 平面BCD.(2)以O点为坐标原点,建立空间直角坐标系,求出平面ACD以及平面BCD的法向量。进而可得出二面角的余弦值以及正切值。
(1)证明易得 OC=3,连接OD,OE,在△OCD中,由余弦定理可得OD=![]() ,
,
因为AD=2![]() ,
,
所以AO2+OD2=AD2,所以AO⊥OD.
同理可证AO⊥OE,又OD∩OE=O,
所以AO⊥平面BCD.
(2)解以O点为原点,建立空间直角坐标系O-xyz(如图).
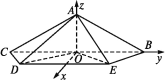
则A(0,0,![]() ),C(0,-3,0),D(1,-2,0),
),C(0,-3,0),D(1,-2,0),
所以![]() =(0,3,
=(0,3,![]() ),
),![]() =(-1,2,
=(-1,2,![]() ).
).
设n=(x,y,z)为平面ACD的法向量,
则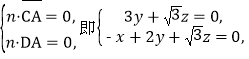
解得![]()
令x=1,得n=(1,-1,![]() ),
),
由(1)知,![]() =(0,0,
=(0,0,![]() )为平面CDB的一个法向量,
)为平面CDB的一个法向量,
所以cos<n,![]() >=
>=![]() ,
,
即二面角A'-CD-B的平面角的正切值为![]() .
.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目