题目内容
【题目】如图,在四棱锥![]() 中,底面ABCD是直角梯形,
中,底面ABCD是直角梯形,![]() ,
,![]() 平面ABCD,
平面ABCD,![]() ,
,![]() .
.
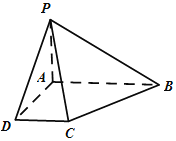
![]() 证明:平面
证明:平面![]() 平面PAC;
平面PAC;
![]() 2
2![]() 若
若![]() ,求二面角
,求二面角![]() 的大小.
的大小.
【答案】(1)见解析;(2)![]()
【解析】
(1)证明![]() ,
,![]() ,推出
,推出![]() 平面
平面![]() ,则平面
,则平面![]() 平面
平面![]() ;
;
(2)由![]() 平面
平面![]() ,得
,得![]() ,
,![]() ,又
,又![]() ,分别以
,分别以![]() ,
,![]() ,
,![]() 所在的直线为
所在的直线为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,由已知向量等式求得
,由已知向量等式求得![]() 的坐标,再分别求出平面
的坐标,再分别求出平面![]() 与平面
与平面![]() 的一个法向量,由两法向量所成角求得二面角
的一个法向量,由两法向量所成角求得二面角![]() 的大小.
的大小.
![]() 证明:
证明:![]() 平面ABCD,
平面ABCD,![]() 平面ABCD,
平面ABCD,![]() .
.
直角梯形ABCD中,
由![]() ,
,![]() ,
,![]() ,
,
得![]() ,则
,则![]() ,即
,即![]() ,
,
又![]() ,
,![]() 平面PAC.
平面PAC.
又![]() 平面PBC,
平面PBC,
![]() 平面
平面![]() 平面PAC;
平面PAC;
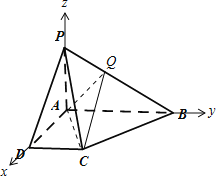
![]() 解:由
解:由![]() 平面ABCD,得
平面ABCD,得![]() ,
,![]() ,又
,又![]() ,
,
分别以AD,AB,AP所在的直线为x轴、y轴、z轴建立空间直角坐标系![]() ,
,
则![]() 0,
0,![]() ,
,![]() 0,
0,![]() ,
,![]() 1,
1,![]() ,
,![]() 2,
2,![]() ,
,
设![]() b,
b,![]() ,由
,由![]() ,得
,得![]() b,
b,![]() ,
,
则![]()
![]() ,
,![]() ,
,
设平面QAC的一个法向量为![]() ,
,
由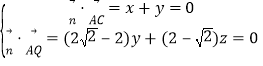 ,取
,取![]() ,则
,则![]() ;
;
平面PAC的一个法向量![]() .
.
![]() ,即
,即![]() .
.
![]() 二面角
二面角![]() 的大小为
的大小为![]() .
.

练习册系列答案
相关题目
【题目】生男生女都一样,女儿也是传后人.由于某些地区仍然存在封建传统思想,头胎的男女情况可能会影响生二孩的意愿,现随机抽取某地200户家庭进行调查统计.这200户家庭中,头胎为女孩的频率为0.5,生二孩的频率为0.525,其中头胎生女孩且生二孩的家庭数为60.
(1)完成下列![]() 列联表:
列联表:
生二孩 | 不生二孩 | 合计 | |
头胎为女孩 | 60 | ||
头胎为男孩 | |||
合计 | 200 |
(2)判断能否有![]() 的把握认为是否生二孩与头胎的男女情况有关;附:
的把握认为是否生二孩与头胎的男女情况有关;附:
| 0,15 | 0.05 | 0.01 | 0.0012.0 |
k | 2.072 | 3.841 | 6.635 | 10.828 |
 (其中
(其中![]() ).
).
【题目】根据以往的经验,某工程施工期间的降水量![]() (单位:
(单位:![]() )对工期的影响如下表:
)对工期的影响如下表:
降水量 |
|
|
|
|
工期延误天数 |
|
|
|
|
历年气象资料表明,该工程施工期间降水量![]() 小于
小于![]() 、
、![]() 、
、![]() 的概率分别为
的概率分别为![]() 、
、![]() 、
、![]() ,求:
,求:
(1)在降水量![]() 至少是
至少是![]() 的条件下,工期延误不超过
的条件下,工期延误不超过![]() 天的概率;
天的概率;
(2)工期延误天数![]() 的均值与方差.
的均值与方差.