题目内容
【题目】已知椭圆![]() 过点
过点 ![]() ,且离心率为
,且离心率为![]() .设
.设![]() 为椭圆
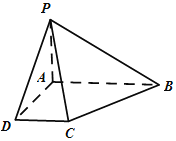
为椭圆![]() 的左、右顶点,P为椭圆上异于
的左、右顶点,P为椭圆上异于![]() 的一点,直线
的一点,直线![]() 分别与直线
分别与直线![]() 相交于
相交于![]() 两点,且直线
两点,且直线![]() 与椭圆
与椭圆![]() 交于另一点
交于另一点![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)求证:直线![]() 与
与![]() 的斜率之积为定值;
的斜率之积为定值;
(Ⅲ)判断三点![]() 是否共线,并证明你的结论.
是否共线,并证明你的结论.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() (Ⅲ)三点共线
(Ⅲ)三点共线
【解析】
(Ⅰ)根据已知条件列a、b、c的方程组,求a、b、c的值,可得椭圆标准方程(Ⅱ)设点P坐标为(x0,y0),将点P的坐标代入椭圆方程可得x0与y0的等量关系,然后利用斜率公式,结合等量关系可证出结论;(Ⅲ)设直线AP的方程为y=k(x﹣2)(k≠0),得直线BP方程,与直线x=2联立,分别求点M、N坐标,然后求直线MN斜率,写直线HM的方程,并与椭圆方程联立,利用韦达定理可求点H坐标,计算AH和AN的斜率,利用这两直线斜率相等来证明结论成立.
解:(Ⅰ)根据题意可知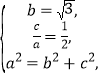 解得
解得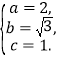
所以椭圆![]() 的方程
的方程![]() .
.
(Ⅱ)根据题意,直线![]() 的斜率都存在且不为零.
的斜率都存在且不为零.
![]() 设
设![]() ,则
,则![]()
![]() .
.
则![]() .
.
因为![]() ,所以
,所以![]() .
.
所以![]() .
.
所以直线![]() 与
与![]() 的斜率之积为定值
的斜率之积为定值![]() .
.
(III)三点![]() 共线.证明如下:
共线.证明如下:
设直线![]() 的方程为
的方程为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() .
.
所以![]() ,
,![]() ,
,![]() .
.
设直线![]() ,
,
联立方程组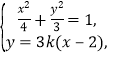 消去
消去![]() 整理得,
整理得,![]() .
.
设![]() ,则
,则![]() 所以
所以![]() ,
,![]() .
.
所以![]() .
.
因为![]() ,
,![]() ,
,
![]() ,
,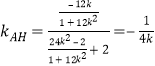 .
.
所以![]() ,所以三点
,所以三点![]() 共线.
共线.

 名校课堂系列答案
名校课堂系列答案【题目】为调研高中生的作文水平.在某市普通高中的某次联考中,参考的文科生与理科生人数之比为![]() ,且成绩分布在
,且成绩分布在![]() 的范围内,规定分数在50以上(含50)的作文被评为“优秀作文”,按文理科用分层抽样的方法抽取400人的成绩作为样本,得到成绩的频率分布直方图,如图所示.其中
的范围内,规定分数在50以上(含50)的作文被评为“优秀作文”,按文理科用分层抽样的方法抽取400人的成绩作为样本,得到成绩的频率分布直方图,如图所示.其中![]() 构成以2为公比的等比数列.
构成以2为公比的等比数列.
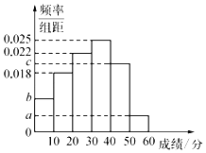
(1)求![]() 的值;
的值;
(2)填写下面![]() 列联表,能否在犯错误的概率不超过0.01的情况下认为“获得优秀作文”与“学生的文理科”有关?
列联表,能否在犯错误的概率不超过0.01的情况下认为“获得优秀作文”与“学生的文理科”有关?
文科生 | 理科生 | 合计 | |
获奖 | 6 | ||
不获奖 | |||
合计 | 400 |
(3)将上述调查所得的频率视为概率,现从全市参考学生中,任意抽取2名学生,记“获得优秀作文”的学生人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附: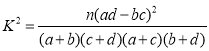 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |