题目内容
【题目】某企业需要建造一个容积为8立方米，深度为2米的无盖长方体水池，已知池壁的造价为每平方米100元，池底造价为每平方米300元，设水池底面一边长为
米，水池总造价为
元，求关于的函数关系式，并求出水池的最低造价.
【答案】
，最低造价为2800元
【解析】
根据已知条件可设底面一边长为
米，则另一边长为
米，蓄水池的总造价为
，再由均值不等式求得最值即可.
由于长方体蓄水池的容积为8立方米，深为2米，
因此其底面积为4平方米，
设底面一边长为米，则另一边长为米，
又因为池壁的造价为每平方米100元，
而池壁的面积为
平方米，
因此池壁的总造价为
，
而池底的造价为每平方米300元，池底的面积为4平方米，因此池底的总造价为1200元，
故蓄水池的总造价为
.
由函数
当且仅当
，即
时，函数
有最小值
，此时总造价最低.
练习册系列答案
名校课堂系列答案
相关题目
【题目】随着我国经济的发展，居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款(年底余额)如下表：
年份 | 2010 | 2011 | 2012 | 2013 | 2014 |
时间代号 | 1 | 2 | 3 | 4 | 5 |
储蓄存款 | 6 | 7 | 8 | 9 | 10 |
(1)求
关于
的回归方程
；
(2)用所求回归方程预测该地区2015年
的人民币储蓄存款.
附：回归方程
中，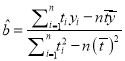 
，
