题目内容
已知等差数列的前三项依次为a，4，3a，前n项和为Sn，且Sk＝110.
(1)求a及k的值；
(2)设数列{bn}的通项bn＝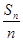
，证明数列{bn}是等差数列，并求其前n项和Tn.
(1)求a及k的值；
(2)设数列{bn}的通项bn＝
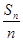，证明数列{bn}是等差数列，并求其前n项和Tn.（1）a＝2，k＝10（2）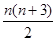
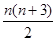
(1)设该等差数列为{an}，则a1＝a，a2＝4，a3＝3a，由已知有a＋3a＝8，得a1＝a＝2，公差d＝4－2＝2，所以Sk＝ka1＋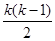
·d＝2k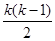＋×2＝k2＋k.由Sk＝110，得k2＋k－110＝0，解得k＝10或k＝－11(舍去)，故a＝2，k＝10.
(2)由(1)Sn＝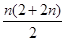
＝n(n＋1)，则bn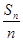＝＝n＋1，故bn＋1－bn＝(n＋2)－(n＋1)＝1，即数列{bn}是首项为2，公差为1的等差数列，所以Tn＝
＝
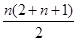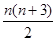
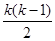·d＝2k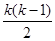＋×2＝k2＋k.由Sk＝110，得k2＋k－110＝0，解得k＝10或k＝－11(舍去)，故a＝2，k＝10.(2)由(1)Sn＝
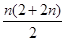＝n(n＋1)，则bn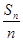＝＝n＋1，故bn＋1－bn＝(n＋2)－(n＋1)＝1，即数列{bn}是首项为2，公差为1的等差数列，所以Tn＝＝
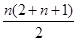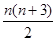
练习册系列答案
相关题目
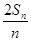＝an＋1－
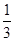n2－n－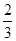
，n∈N*.
.
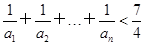是点集A到点集B的一个映射，且对任意
，有
.现对点集A中的点
，
，均有
，点
为（0,2），则线段
的长度
.
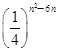(n∈N*)，bn＝log2an，则数列{bn}的前n项和Sn取最大时，n＝________．
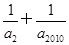的最小值为________．
，……，
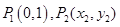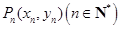．若点
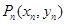到点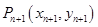
的变化关系为：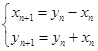
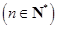，则
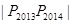等于 ．