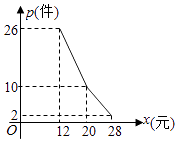题目内容
【题目】如图，记正方形ABCD四条边的中点为S，M，N，T，连接四个中点得小正方形SMNT．将正方形ABCD，正方形SMNT绕对角线AC旋转一周得到的两个旋转体的体积依次记为V1 ， V2 ， 则V1：V2=（ ）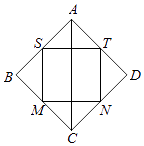 
A.8：1
B.2：1
C.4：3
D.8：3
【答案】D
【解析】解：将正方形ABCD绕对角线AC旋转一周得到的旋转体为同底的两个圆锥的组合体，将正方形SMNT绕AC旋转一周得到的几何体为圆柱．
设正方形SMNT的边长为1，则正方形ABCD的边长为 
，则圆锥的底面半径和高均为1，圆柱的底面半径为 
，高为1．
则V1= 
= 
，V2= 
= 
．∴ 
= 
．
故选：D．
【考点精析】关于本题考查的旋转体（圆柱、圆锥、圆台），需要了解常见的旋转体有：圆柱、圆锥、圆台、球才能得出正确答案．
练习册系列答案
阳光课堂同步练习系列答案
相关题目
【题目】某地西红柿从 
月 
日起开始上市．通过市场调查，得到西红柿种植成本 
(就是每 
公斤西红柿的种植成本，单位：元)与上市时间 
(单位：天)的数据如下表：
上市时间 | 50 | 110 | 250 |
种植成本 | 150 | 108 | 150 |
（1）根据上表数据，从下列函数中选取一个函数描述西红柿种植成本与上市时间 的变化关系： 
； 
； 
； 
，并求出函数解析式；
（2）利用你选取的函数，求西红柿种植成本最低时的上市天数及最低种植成本．
