Question

【题目】设函数f′（x）是奇函数f（x）（x∈R）的导函数，f（﹣1）=0，当x＞0时，xf′（x）﹣f（x）＜0，则使得f（x）＞0成立的x的取值范围是（ ）
A.（﹣∞，﹣1）∪（0，1）
B.（﹣1，0）∪（1，+∞）
C.（﹣∞，﹣1）∪（﹣1，0）
D.（0，1）∪（1，+∞）

Answer 1

【答案】A
【解析】解：设g（x）= ，则g（x）的导数为：g′（x）= ， ∵当x＞0时总有xf′（x）＜f（x）成立，
即当x＞0时，g′（x）恒小于0，
∴当x＞0时，函数g（x）= 为减函数，
又∵g（﹣x）= = = =g（x），
∴函数g（x）为定义域上的偶函数
又∵g（﹣1）= =0，
∴函数g（x）的图象性质类似如图：
数形结合可得，不等式f（x）＞0xg（x）＞0
或 ，
0＜x＜1或x＜﹣1．
故选：A．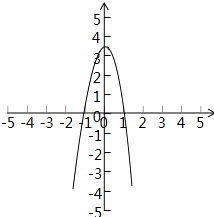

由已知当x＞0时总有xf′（x）﹣f（x）＜0成立，可判断函数g（x）= 为减函数，由已知f（x）是定义在R上的奇函数，可证明g（x）为（﹣∞，0）∪（0，+∞）上的偶函数，根据函数g（x）在（0，+∞）上的单调性和奇偶性，模拟g（x）的图象，而不等式f（x）＞0等价于xg（x）＞0，数形结合解不等式组即可．