题目内容
(本小题满分10分)
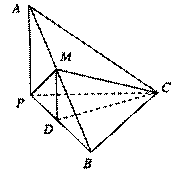
已知四棱锥P—ABCD的底面为直角梯形,AB//DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=1,AB=2,M是PB的中点。
(I)求AC与PB所 成角的余弦值;
成角的余弦值;
(II)求面AMC与面BMC所成二面角的余弦值的大小。
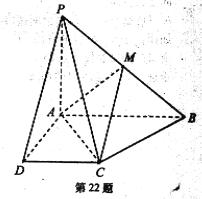
已知四棱锥P—ABCD的底面为直角梯形,AB//DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=1,AB=2,M是PB的中点。
(I)求AC与PB所
 成角的余弦值;
成角的余弦值;(II)求面AMC与面BMC所成二面角的余弦值的大小。

(I)AC与PB所成的角的余弦值为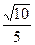
(II)面AMC与 面BMC二面角的余弦值为
面BMC二面角的余弦值为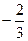
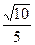
(II)面AMC与
 面BMC二面角的余弦值为
面BMC二面角的余弦值为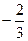
解:以A为坐标原点AD、AB、AP所在直线分别为x轴、y轴、z轴建立空间直角坐标系,则各点坐标为 ………2分
………2分
(I)因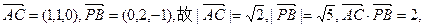
所以
即AC与PB所成的角的余弦值为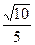 ………
……… ………6分
………6分
(II)由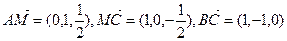 ,
,
设平面AMC与面BMC的法向量分别为 ,
,
则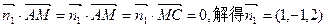 ,
,
同理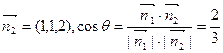 ………………8分
………………8分
由题意可知 ,二面角的平面角为钝角,
,二面角的平面角为钝角,
所以面AMC与 面BMC二面角的余弦值为
面BMC二面角的余弦值为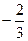 ………………10分
………………10分
 ………2分
………2分(I)因
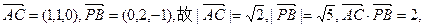
所以

即AC与PB所成的角的余弦值为
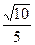 ………
……… ………6分
………6分(II)由
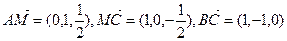 ,
,设平面AMC与面BMC的法向量分别为
 ,
,则
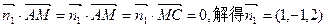 ,
,同理
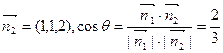 ………………8分
………………8分由题意可知
 ,二面角的平面角为钝角,
,二面角的平面角为钝角,所以面AMC与
 面BMC二面角的余弦值为
面BMC二面角的余弦值为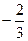 ………………10分
………………10分
练习册系列答案
 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
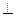 底面ABCD,PA=AB=
底面ABCD,PA=AB=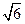 ,点E是棱PB的中点。(1)求直线AD与平面PBC的距离。
,点E是棱PB的中点。(1)求直线AD与平面PBC的距离。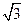 ,求二面角A-EC-D的平面角的余弦值。
,求二面角A-EC-D的平面角的余弦值。
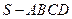 的底面是边长为
的底面是边长为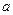 的正方形,且
的正方形,且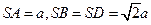 。
。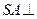 平面
平面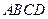 ;
;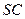 为四棱锥中最长的侧棱,点
为四棱锥中最长的侧棱,点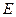 为
为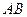 的中点.求直线SE.与平面SAC所成角的正弦值。
的中点.求直线SE.与平面SAC所成角的正弦值。
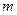 、
、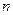 与平面
与平面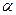 、
、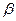 ,有下列四个命题:
,有下列四个命题: 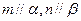 且
且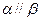 ,则
,则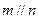 ; ②
; ②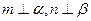 且
且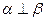 ,则
,则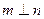 ;
;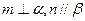 且
且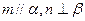 且
且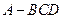 中,
中,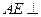 平面
平面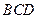 ,
,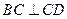 ,
,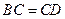 ,
,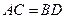 ,
,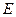 是
是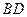 的中点;
的中点;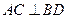 ;
;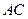 与平面
与平面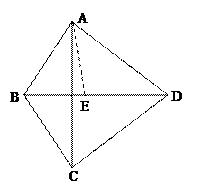
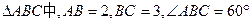 ,AD为BC边上的高,O为AD的中点,若
,AD为BC边上的高,O为AD的中点,若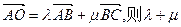 = .
= .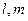 是两条不同的直线,
是两条不同的直线,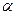 是一个平面,则下列命题错误的是 .
是一个平面,则下列命题错误的是 .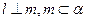 ,则
,则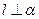 ;②若
;②若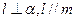 ,则
,则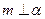 ;
;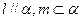 ,则
,则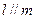 ;④若
;④若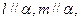 ,则
,则