题目内容
(本小题满分12分)
一个四棱锥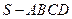 的底面是边长为
的底面是边长为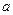 的正方形,且
的正方形,且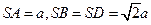 。
。
(1)求证: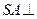 平面
平面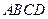 ;
;
(2)若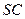 为四棱锥中最长的侧棱,点
为四棱锥中最长的侧棱,点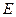 为
为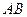 的中点.求直线SE.与平面SAC所成角的正弦值。
的中点.求直线SE.与平面SAC所成角的正弦值。
一个四棱锥
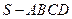 的底面是边长为
的底面是边长为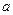 的正方形,且
的正方形,且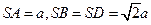 。
。(1)求证:
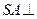 平面
平面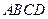 ;
;(2)若
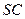 为四棱锥中最长的侧棱,点
为四棱锥中最长的侧棱,点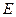 为
为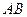 的中点.求直线SE.与平面SAC所成角的正弦值。
的中点.求直线SE.与平面SAC所成角的正弦值。
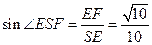
(1)证明: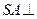 平面
平面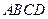 ,
,
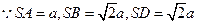
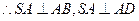 ,∴
,∴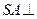 平面
平面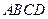 . ….6分
. ….6分
(2)解:作EF⊥AC交于 F,连接SF,易证EF⊥SA ∴EF⊥平面SAC( 8分)
∴∠ESF是直线SE.与平面SAC所成角。
EF=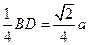 SE=
SE=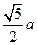 (10分)
(10分)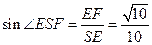 ….12分
….12分
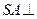 平面
平面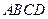 ,
,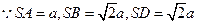
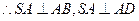 ,∴
,∴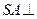 平面
平面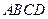 . ….6分
. ….6分(2)解:作EF⊥AC交于 F,连接SF,易证EF⊥SA ∴EF⊥平面SAC( 8分)
∴∠ESF是直线SE.与平面SAC所成角。
EF=
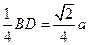 SE=
SE=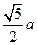 (10分)
(10分)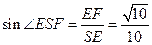 ….12分
….12分
练习册系列答案
相关题目
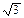 的圆柱,求圆柱的表面积
的圆柱,求圆柱的表面积
 成角的余弦值;
成角的余弦值;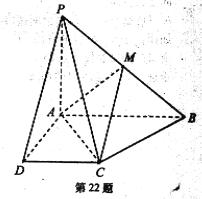
 AB,N为AB
AB,N为AB 上一点,
上一点,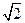 .
.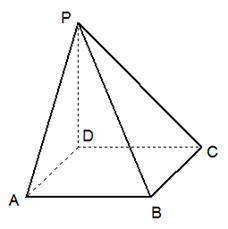
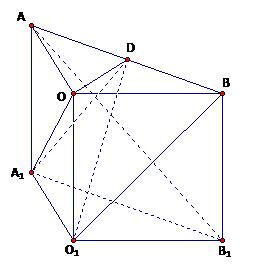
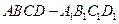 的棱长为
的棱长为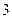 ,点
,点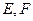 在线段
在线段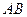 上,点
上,点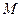 在线段
在线段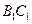 上,点
上,点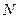 在线段
在线段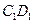 上,且
上,且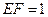 ,
,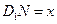 ,
,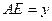 ,
,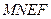 的体积( )
的体积( )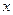 有关,与
有关,与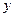 无关
无关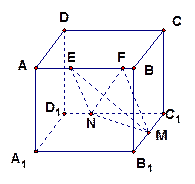

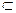 α,m
α,m