题目内容
【题目】某工厂生产某种型号的农机具零配件,为了预测今年7月份该型号农机具零配件的市场需求量,以合理安排生产,工厂对本年度1月份至6月份该型号农机具零配件的销售量及销售单价进行了调查,销售单价![]() (单位:元)和销售量
(单位:元)和销售量![]() (单位:千件)之间的6组数据如下表所示:
(单位:千件)之间的6组数据如下表所示:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
销售单价 | 11.1 | 9.1 | 9.4 | 10.2 | 8.8 | 11.4 |
销售量 | 2.5 | 3.1 | 3 | 2.8 | 3.2 | 2.4 |
(1)根据1至6月份的数据,求![]() 关于
关于![]() 的线性回归方程(系数精确到0.01);
的线性回归方程(系数精确到0.01);
(2)结合(1)中的线性回归方程,假设该型号农机具零配件的生产成本为每件3元,那么工厂如何制定7月份的销售单价,才能使该月利润达到最大?(计算结果精确到0.1)
参考公式:回归直线方程![]() ,
,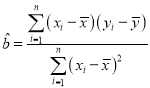
参考数据:![]() ,
,![]()
【答案】(1)![]() ;(2)销售单价为11.3元时,该月利润才能达到最大
;(2)销售单价为11.3元时,该月利润才能达到最大
【解析】
(1)求出![]() 的平均数,利用最小二乘法即可得出
的平均数,利用最小二乘法即可得出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)由题意得出7月份的利润的关系式,结合二次函数的性质,即可得出结论.
(1)由条件知,![]() ,
,![]()
所以 ,
,![]()
故![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() .
.
(2)假设7月份的销售单价为![]() 元
元
则由(1)可知,7月份零配件销量为![]()
故7月份的利润![]() ,
,
其对称轴![]() ,故7月份销售单价为11.3元时,该月利润才能达到最大.
,故7月份销售单价为11.3元时,该月利润才能达到最大.

【题目】2019年9月23日,在![]() 省
省![]() 市举办的2019年中国农民丰收节“新电商与农业科技创新”论坛上,来自政府相关部门的领导及11所中国高校的专家学者以“农业科技创新与乡村振兴”、“新农人与脱贫攻坚”为核心议题各抒己见,农产品方面的科技创新越来越成为21世纪大国崛起的一项重大突破.科学家对某农产品每日平均增重量
市举办的2019年中国农民丰收节“新电商与农业科技创新”论坛上,来自政府相关部门的领导及11所中国高校的专家学者以“农业科技创新与乡村振兴”、“新农人与脱贫攻坚”为核心议题各抒己见,农产品方面的科技创新越来越成为21世纪大国崛起的一项重大突破.科学家对某农产品每日平均增重量![]() (单位:
(单位:![]() )与每日营养液注射量
)与每日营养液注射量![]() (单位:
(单位:![]() )之间的关系统计出表1一组数据:
)之间的关系统计出表1一组数据:
表1
| 1 | 2 | 3 | 4 | 5 |
| 2 | 3.5 | 5 | 6.6 | 8.4 |
(1)根据表1和表2的相关统计值求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)计算拟合指数![]() 的值,并说明线性回归模型的拟合效果(
的值,并说明线性回归模型的拟合效果(![]() 的值在.98以上说明拟合程度好);
的值在.98以上说明拟合程度好);
(3)若某日该农产品的营养液注释量为![]() ,预测该日这种农产品的平均增长重量(结果精确到0.1).
,预测该日这种农产品的平均增长重量(结果精确到0.1).
附:①
表2
|
|
|
|
92.4 | 55 | 25 | 0.04 |
②对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: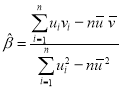 ,
,![]() ,
,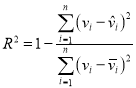 .
.
【题目】某公司培训员工某项技能,培训有如下两种方式,方式一:周一到周五每天培训1小时,周日测试;方式二:周六一天培训4小时,周日测试.公司有多个班组,每个班组60人,现任选两组(记为甲组、乙组)先培训,甲组选方式一,乙组选方式二,并记录每周培训后测试达标的人数如下表,其中第一、二周达标的员工评为优秀.
第一周 | 第二周 | 第三周 | 第四周 | |
甲组 | 20 | 25 | 10 | 5 |
乙组 | 8 | 16 | 20 | 16 |
(1)在甲组内任选两人,求恰有一人优秀的概率;
(2)每个员工技能测试是否达标相互独立,以频率作为概率.
(i)设公司员工在方式一、二下的受训时间分别为![]() 、
、![]() ,求
,求![]() 、
、![]() 的分布列,若选平均受训时间少的,则公司应选哪种培训方式?
的分布列,若选平均受训时间少的,则公司应选哪种培训方式?
(ii)按(i)中所选方式从公司任选两人,求恰有一人优秀的概率.