题目内容
【题目】设函数![]() ,
,![]() ,
,![]() .
.
(1)若对任意![]() ,
,![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(2)![]() ,讨论函数
,讨论函数![]() 的单调性.
的单调性.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)将对任意![]() ,
,![]() 恒成立,转化为对任意
恒成立,转化为对任意![]() ,
, ![]() 恒成立,令
恒成立,令![]() ,由函数
,由函数![]() 在区间
在区间![]() 上单调递减,只需证
上单调递减,只需证![]() 恒成立即可.
恒成立即可.
(2)得到![]() ,求导
,求导![]() ,再分
,再分![]() ,
,![]() ,
, ![]() ,
, ![]() ,
,![]() 五种情况讨论求解.
五种情况讨论求解.
(1)因为![]() ,
,![]() ,即
,即![]() ,
,
即![]() ,
,
令![]() ,
,
因为函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
所以![]() 恒成立,
恒成立,
即![]() 在区间
在区间![]() 上恒成立,
上恒成立,
故![]() .
.
(2)![]() ,
,
![]() ,
,
当![]() 时,
时,![]() ,
,
![]() ,
,![]() ,
,![]() 递增,
递增,![]() ,
,![]() ,
,![]() 递减,
递减,
当![]() 时,
时,![]() ,
,
![]() ,
,![]() ,
,![]() 递增,
递增,![]() ,
,![]() ,
,![]() 递减,
递减,
当![]() 时,
时,![]() ,
,![]() 的单调递增区间为
的单调递增区间为![]() ,
,
当![]() 时,
时,![]() ,
,![]() 或
或![]() ;
;![]() ,当
,当![]() 变化,
变化,![]() ,
,![]() 变化如下表
变化如下表
|
|
|
| 1 |
|
| 正 | 零 | 负 | 零 | 正 |
| 递增 | 极大值 | 递减 | 极小值 | 递增 |
即单调增区间为![]() ,
,![]() ,减区间为
,减区间为![]() .
.
当![]() 时,
时,![]() ,
,![]() 或
或![]() ;
;![]() ,当
,当![]() 变化,
变化,![]() ,
,![]() 变化如下表
变化如下表
|
| 1 |
|
|
|
| 正 | 零 | 负 | 零 | 正 |
| 递增 | 极大值 | 递减 | 极小值 | 递增 |
即单调增区间为![]() ,
,![]() ,减区间为
,减区间为![]() .
.
综上:当![]() 时,单调增区间为
时,单调增区间为![]() ,减区间为
,减区间为![]() ,
,
当![]() 时,单调增区间为
时,单调增区间为![]() ,
,![]() ,减区间为
,减区间为![]() ,
,
当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,
,
当![]() 时,单调增区间为
时,单调增区间为![]() ,
,![]() ,减区间为
,减区间为![]() .
.

【题目】某工厂生产某种型号的农机具零配件,为了预测今年7月份该型号农机具零配件的市场需求量,以合理安排生产,工厂对本年度1月份至6月份该型号农机具零配件的销售量及销售单价进行了调查,销售单价![]() (单位:元)和销售量
(单位:元)和销售量![]() (单位:千件)之间的6组数据如下表所示:
(单位:千件)之间的6组数据如下表所示:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
销售单价 | 11.1 | 9.1 | 9.4 | 10.2 | 8.8 | 11.4 |
销售量 | 2.5 | 3.1 | 3 | 2.8 | 3.2 | 2.4 |
(1)根据1至6月份的数据,求![]() 关于
关于![]() 的线性回归方程(系数精确到0.01);
的线性回归方程(系数精确到0.01);
(2)结合(1)中的线性回归方程,假设该型号农机具零配件的生产成本为每件3元,那么工厂如何制定7月份的销售单价,才能使该月利润达到最大?(计算结果精确到0.1)
参考公式:回归直线方程![]() ,
,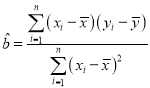
参考数据:![]() ,
,![]()
【题目】下表为![]() 年至
年至![]() 年某百货零售企业的线下销售额(单位:万元),其中年份代码
年某百货零售企业的线下销售额(单位:万元),其中年份代码![]() 年份
年份![]() .
.
年份代码 |
|
|
|
|
线下销售额 |
|
|
|
|
(1)已知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程,并预测
的线性回归方程,并预测![]() 年该百货零售企业的线下销售额;
年该百货零售企业的线下销售额;
(2)随着网络购物的飞速发展,有不少顾客对该百货零售企业的线下销售额持续增长表示怀疑,某调查平台为了解顾客对该百货零售企业的线下销售额持续增长的看法,随机调查了![]() 位男顾客、
位男顾客、![]() 位女顾客(每位顾客从“持乐观态度”和“持不乐观态度”中任选一种),其中对该百货零售企业的线下销售额持续增长持乐观态度的男顾客有
位女顾客(每位顾客从“持乐观态度”和“持不乐观态度”中任选一种),其中对该百货零售企业的线下销售额持续增长持乐观态度的男顾客有![]() 人、女顾客有
人、女顾客有![]() 人,能否在犯错误的概率不超过
人,能否在犯错误的概率不超过![]() 的前提下认为对该百货零售企业的线下销售额持续增长所持的态度与性别有关?
的前提下认为对该百货零售企业的线下销售额持续增长所持的态度与性别有关?
参考公式及数据: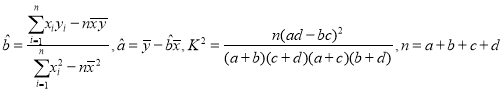 .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|