题目内容
【题目】已知函数![]() ,其中
,其中![]() .
.
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)求证: 当![]() 时,
时,![]() .
.
【答案】(Ⅰ)y=2e (Ⅱ)见证明
【解析】
(Ⅰ)求出导函数,求出切点坐标,切线的斜率,然后求解曲线y=f(x)在(﹣1,f(﹣1))处的切线方程;
(Ⅱ)法一:![]() ,令f'(x)=0,求出极值点,判断导函数的符号,得到函数的单调性,求出函数的最小值,只需证明
,令f'(x)=0,求出极值点,判断导函数的符号,得到函数的单调性,求出函数的最小值,只需证明![]() ,
,![]() ,
,![]() ,设
,设![]() ,其中x>2,利用导函数转化求解即可;
,其中x>2,利用导函数转化求解即可;
法二:设![]() ,其中x>0,
,其中x>0,![]() ,推出F(x)在区间(0,2)上单调递减,在(2,+∞)上单调递增,所以函数F(x)在x=2时取得最小值
,推出F(x)在区间(0,2)上单调递减,在(2,+∞)上单调递增,所以函数F(x)在x=2时取得最小值![]() ,而
,而![]() ,推出结果即可;
,推出结果即可;
法三:因为“对任意的x>0,![]() ”等价于“对任意的x>0,
”等价于“对任意的x>0,![]() ”,只需证“x>0时,2ex+e(a﹣x2)>0”,设g(x)=2ex+e(a﹣x2),其中x≥0,g'(x)=2ex﹣2ex,设h(x)=g'(x),h'(x)=2ex﹣2e,求出函数的极小值,通过g(x)在(0,+∞)上单调递增,得g(x)>g(0),转化证明即可.
”,只需证“x>0时,2ex+e(a﹣x2)>0”,设g(x)=2ex+e(a﹣x2),其中x≥0,g'(x)=2ex﹣2ex,设h(x)=g'(x),h'(x)=2ex﹣2e,求出函数的极小值,通过g(x)在(0,+∞)上单调递增,得g(x)>g(0),转化证明即可.
(Ⅰ)因为![]()
所以![]()
当![]() 时,
时,![]()
所以![]() ,而
,而![]()
曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]()
(Ⅱ)法一:
因为![]() ,令
,令![]()
得![]()
显然当![]() 时,
时,![]()
所以![]() ,
,![]() ,
,![]() 在区间
在区间![]() 上的变化情况如下表:
上的变化情况如下表:
|
|
|
|
|
| 0 |
|
|
| 极小值 |
|
所以![]() 在区间
在区间![]() 上单调递减,在
上单调递减,在![]() 单调递增,
单调递增,
所以![]() 在
在![]() 上的最小值为
上的最小值为![]() ,所以只需证明
,所以只需证明![]()
因为![]() ,所以
,所以![]()
设![]() ,其中
,其中![]()
所以![]()
当![]() 时,
时,![]() ,所以
,所以![]() 在区间
在区间![]() 单调递增,
单调递增,
因为 ![]() ,所以
,所以![]() ,问题得证
,问题得证
法二:
因为![]() ,所以当
,所以当![]() 时,
时,![]()
设![]() ,其中
,其中![]()
所以![]()
所以![]() ,
,![]() ,
,![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
| 0 |
|
|
| 极小值 |
|
所以![]() 在区间
在区间![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以函数![]() 在
在![]() 时取得最小值
时取得最小值![]() ,而
,而![]()
所以![]() 时
时![]()
所以![]() ,问题得证
,问题得证
法三:
因为“对任意的![]() ,
,![]() ”等价于“对任意的
”等价于“对任意的![]() ,
,![]() ”
”
即“![]() ,
,![]() ”,故只需证“
”,故只需证“![]() 时,
时,![]() ”
”
设![]() ,其中
,其中![]()
所以![]()
设![]() ,
,![]() ,
,
令![]() ,得
,得![]()
所以![]() ,
,![]() ,
,![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
| 0 |
|
|
| 极小值 |
|
所以![]() 在
在![]() 处取得极小值,而
处取得极小值,而![]()
所以![]()
所以![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递增,得
上单调递增,得![]()
而![]() ,所以
,所以![]() 问题得证
问题得证

【题目】某校的一个社会实践调查小组,在对该校学生的良好“用眼习惯”的调查中,随机发放了120分问卷.
对收回的100份有效问卷进行统计,得到如下2×2列联表:
做不到科学用眼 | 能做到科学用眼 | 合计 | |
男 | 45 |
|
|
女 |
| 15 |
|
合计 |
|
| 100 |
(1)求上表中的x
(2)若在犯错误的概率不超过P的前提下认为良好“用眼习惯”与性别有关,那么根据临界值表,最精确的P的值应为多少?
附:独立性检验统计量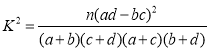 ,其中
,其中![]() .
.
独立性检验临界值表:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.840 | 5.024 |
【题目】某工厂生产某种型号的农机具零配件,为了预测今年7月份该型号农机具零配件的市场需求量,以合理安排生产,工厂对本年度1月份至6月份该型号农机具零配件的销售量及销售单价进行了调查,销售单价![]() (单位:元)和销售量
(单位:元)和销售量![]() (单位:千件)之间的6组数据如下表所示:
(单位:千件)之间的6组数据如下表所示:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
销售单价 | 11.1 | 9.1 | 9.4 | 10.2 | 8.8 | 11.4 |
销售量 | 2.5 | 3.1 | 3 | 2.8 | 3.2 | 2.4 |
(1)根据1至6月份的数据,求![]() 关于
关于![]() 的线性回归方程(系数精确到0.01);
的线性回归方程(系数精确到0.01);
(2)结合(1)中的线性回归方程,假设该型号农机具零配件的生产成本为每件3元,那么工厂如何制定7月份的销售单价,才能使该月利润达到最大?(计算结果精确到0.1)
参考公式:回归直线方程![]() ,
,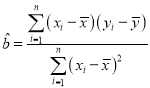
参考数据:![]() ,
,![]()
【题目】下表为![]() 年至
年至![]() 年某百货零售企业的线下销售额(单位:万元),其中年份代码
年某百货零售企业的线下销售额(单位:万元),其中年份代码![]() 年份
年份![]() .
.
年份代码 |
|
|
|
|
线下销售额 |
|
|
|
|
(1)已知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程,并预测
的线性回归方程,并预测![]() 年该百货零售企业的线下销售额;
年该百货零售企业的线下销售额;
(2)随着网络购物的飞速发展,有不少顾客对该百货零售企业的线下销售额持续增长表示怀疑,某调查平台为了解顾客对该百货零售企业的线下销售额持续增长的看法,随机调查了![]() 位男顾客、
位男顾客、![]() 位女顾客(每位顾客从“持乐观态度”和“持不乐观态度”中任选一种),其中对该百货零售企业的线下销售额持续增长持乐观态度的男顾客有
位女顾客(每位顾客从“持乐观态度”和“持不乐观态度”中任选一种),其中对该百货零售企业的线下销售额持续增长持乐观态度的男顾客有![]() 人、女顾客有
人、女顾客有![]() 人,能否在犯错误的概率不超过
人,能否在犯错误的概率不超过![]() 的前提下认为对该百货零售企业的线下销售额持续增长所持的态度与性别有关?
的前提下认为对该百货零售企业的线下销售额持续增长所持的态度与性别有关?
参考公式及数据: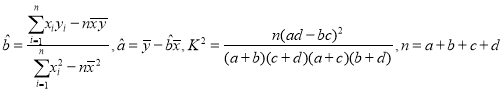 .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|

