题目内容
【题目】已知函数f(x)= ![]() 若存在实数b,使函数g(x)=f(x)﹣b有两个零点,则a的取值范围是 .
若存在实数b,使函数g(x)=f(x)﹣b有两个零点,则a的取值范围是 .
【答案】{a|a<0或a>1}
【解析】解:∵g(x)=f(x)﹣b有两个零点,
∴f(x)=b有两个零点,即y=f(x)与y=b的图像有两个交点,
由x3=x2可得,x=0或x=1
①当a>1时,函数f(x)的图像如图所示,此时存在b,满足题意,故a>1满足题意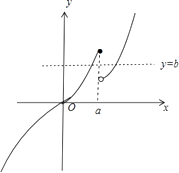
②当a=1时,由于函数f(x)在定义域R上单调递增,故不符合题意
③当0<a<1时,函数f(x)单调递增,故不符合题意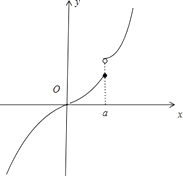
④a=0时,f(x)单调递增,故不符合题意
⑤当a<0时,函数y=f(x)的图像如图所示,此时存在b使得,y=f(x)与y=b有两个交点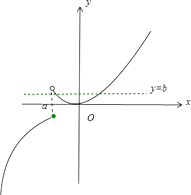
综上可得,a<0或a>1
所以答案是:{a|a<0或a>1}
【考点精析】本题主要考查了函数的零点的相关知识点,需要掌握函数的零点就是方程的实数根,亦即函数的图象与轴交点的横坐标.即:方程有实数根,函数的图象与坐标轴有交点,函数有零点才能正确解答此题.

练习册系列答案
相关题目
【题目】某海滨浴场每年夏季每天的海浪高度y(米)是时间x(0≤x≤24,单位:小时)的函数,记作y=f(x),下表是每年夏季每天某些时刻的浪高数据:
x(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
y(米) | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 |
(1)经观察发现可以用三角函数y=Acosωx+b对这些数据进行拟合,求函数f(x)的表达式;
(2)浴场规定,每天白天当海浪高度高于1.25米时,才对冲浪爱好者开放,求冲浪者每天白天可以在哪个时段到该浴场进行冲浪运动?