题目内容
【题目】
=（sinx，cosx）， 
=（sinx，sinx）， 
=（﹣1，0）
（1）若x= 
，求 与 的夹角θ；
（2）若x∈[﹣ 
， 
]，f（x）=λ 的最大值为 
，求λ．
【答案】
（1）
解：当x= 
时， 
=（ 
， 
）， 
=（﹣1，0），
∴ 与 的夹角θ满足cosθ= 
=- ，
∴ 与 的夹角θ= 
；
（2）
解：f（x）=λ 
=λ（sin2x+sinxcosx）
=λ（ 
+ sin2x）= 
λsin（2x﹣ 
）+ λ，
∵x∈[﹣ 
， ]，∴2x﹣ ∈[﹣π， ]，
∴sin（2x﹣ ）∈[﹣1， ]，
当λ＞0时，可得 λ /span> + λ= ，解得λ= ；
当λ＜0时，可得 λ（﹣1）+ λ= ，解得λ=﹣ 
﹣1
【解析】（1）当x= 时可得 =（ ， ）， =（﹣1，0），由夹角公式可得；（2）可得f（x）=λ = λsin（2x﹣ ）+ λ，由x的范围易得sin（2x﹣ ）∈[﹣1， ]，分类讨论可得．
【考点精析】认真审题，首先需要了解数量积表示两个向量的夹角(设
、
都是非零向量，
，
，
是与
的夹角，则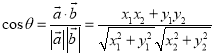
)，还要掌握两角和与差的正弦公式(两角和与差的正弦公式：
)的相关知识才是答题的关键．
练习册系列答案
相关题目
