题目内容
【题目】某企业生产甲、乙两种产品均需用A,B两种原料,已知每种产品各生产1吨所需原料及每天原料的可用限额如下表所示,如果生产1吨甲产品可获利润3万元,生产1吨乙产品可获利4万元,则该企业每天可获得最大利润为万元.
甲 | 乙 | 原料限额 | |
A(吨) | 3 | 2 | 12 |
B(吨) | 1 | 2 | 8 |
【答案】18
【解析】解:设每天生产甲乙两种产品分别为x,y吨,利润为z元, 则 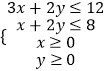 ,
,
目标函数为 z=3x+4y.
作出二元一次不等式组所表示的平面区域(阴影部分)即可行域.
由z=3x+4y得y=﹣ ![]() x+
x+ ![]() z,
z,
平移直线y=﹣ ![]() x+
x+ ![]() z
z
由图象可知当直线y=﹣ ![]() x+
x+ ![]() z经过点B时,
z经过点B时,
直线y=﹣ ![]() x+
x+ ![]() z的截距最大,
z的截距最大,
此时z最大,
解方程组 ![]() ,解得x=2y=3,
,解得x=2y=3,
即B的坐标为(2,3),
∴zmax=3x+4y=6+12=18.
即每天生产甲乙两种产品分别为2,3吨,能够产生最大的利润,最大的利润是18万元,
故答案为:18.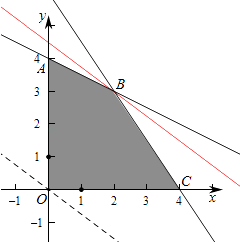
设每天生产甲乙两种产品分别为x,y吨,利润为z元,根据题目条件建立约束条件,
得到目标函数,画出约束条件所表示的区域,再利用平移法求出z的最大值.

练习册系列答案
相关题目
【题目】从某高中随机选取5名高一男生,其身高和体重的数据如表所示:
身高x(cm) | 160 | 165 | 170 | 175 | 180 |
体重y(kg) | 63 | 66 | 70 | 72 | 74 |
根据如表可得回归方程 ![]() =0.56x+
=0.56x+ ![]() ,据此模型可预报身高为172cm的高一男生的体重为( )
,据此模型可预报身高为172cm的高一男生的体重为( )
A.70.12kg
B.70.29kg
C.70.55kg
D.71.05kg