题目内容
【题目】直三棱柱A1B1C1﹣ABC,∠BCA=90°,点D1 , F1分别是A1B1 , A1C1的中点,BC=CA=CC1 , 则BD1与AF1所成角的余弦值是( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:∵直三棱柱A1B1C1﹣ABC,∠BCA=90°, ∴以C为原点,CA为x轴,CB为y轴,CC1为z轴,建立空间直角坐标系,
∵点D1 , F1分别是A1B1 , A1C1的中点,BC=CA=CC1 ,
∴设BC=CA=CC1=2,
则B(0,20),D1(1,1,2),A(2,0,0),F1(1,0,2),![]() =(1,﹣1,2),
=(1,﹣1,2), ![]() =(﹣1,0,2),
=(﹣1,0,2),
设BD1与AF1所成角为θ,
则cosθ=  =
= ![]() =
= ![]() .
.
∴BD1与AF1所成角的余弦值为 ![]() .
.
故选:B.
【考点精析】解答此题的关键在于理解异面直线及其所成的角的相关知识,掌握异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系.

练习册系列答案
相关题目
【题目】某种产品的广告费支出x与销售额y(单位:百万元)之间有如下对应数据:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
参考公式:b= 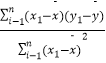 =
= 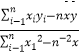 .
.
(1)画出散点图;
(2)求回归直线方程;
(3)试预测广告费支出为10百万元时,销售额多大?