题目内容
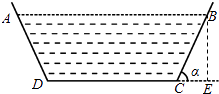
【题目】2015年春,某地干旱少雨,农作物受灾严重,为了使今后保证农田灌溉,当地政府决定建一横断面为等腰梯形的水渠(水渠的横断面如图所示),为减少水的流失量,必须减少水与渠壁的接触面,若水渠横断面的面积设计为定值S,渠深为h,则水渠壁的倾斜角α(0<α< ![]() )为多大时,水渠中水的流失量最小?
)为多大时,水渠中水的流失量最小?
【答案】解:作BE⊥DC于E,在Rt△BEC中,BC= ![]() ,CE=hcotα,又AB﹣CD=2CE=2hcotα,AB+CD=
,CE=hcotα,又AB﹣CD=2CE=2hcotα,AB+CD= ![]() ,故CD=
,故CD= ![]() ﹣hcotα.
﹣hcotα.
设y=AD+DC+BC,则y= ![]() ﹣hcotα+
﹣hcotα+ ![]() =
= ![]() +
+ ![]() (0<α<
(0<α< ![]() ),
),
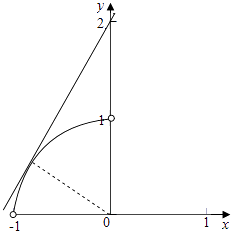
由于S与h是常量,欲使y最小,只需u= ![]() 取最小值,u可看作(0,2)与(﹣sinα,cosα)两点连线的斜率,由于α∈(0,
取最小值,u可看作(0,2)与(﹣sinα,cosα)两点连线的斜率,由于α∈(0, ![]() ),点(﹣sinα,cosα)在曲线x2+y2=1(﹣1<x<0,0<y<1)上运动,当过(0,2)的直线与曲线相切时,直线斜率最小,此时切点为(﹣
),点(﹣sinα,cosα)在曲线x2+y2=1(﹣1<x<0,0<y<1)上运动,当过(0,2)的直线与曲线相切时,直线斜率最小,此时切点为(﹣ ![]() ,
, ![]() ),则有sinα=
),则有sinα= ![]() ,且cosα=
,且cosα= ![]() ,那么α=
,那么α= ![]() ,
,
故当α= ![]() 时,水渠中水的流失量最小.
时,水渠中水的流失量最小.
【解析】由题意可得作BE⊥DC于E,在Rt△BEC中,求得BC= ![]() ,CE=hcotα,又AB﹣CD=2CE=2hcotα,AB+CD=
,CE=hcotα,又AB﹣CD=2CE=2hcotα,AB+CD= ![]() ,故CD= S h ﹣hcotα.
,故CD= S h ﹣hcotα.
设y=AD+DC+BC则y= ![]() ﹣hcotα+
﹣hcotα+ ![]() =
= ![]() +
+ ![]() (0<α<
(0<α< ![]() )当
)当![]() 取最小值两点连线的斜率,由于α∈(0,
取最小值两点连线的斜率,由于α∈(0, ![]() ),点(﹣sinα,cosα)在曲线x2+y2=1(﹣1<x<0,0<y<1)上运动当过(0,2)的直线与曲线相切时,直线斜率最小,此时切点为(﹣
),点(﹣sinα,cosα)在曲线x2+y2=1(﹣1<x<0,0<y<1)上运动当过(0,2)的直线与曲线相切时,直线斜率最小,此时切点为(﹣ ![]() ,
, ![]() ),则有sinα=
),则有sinα=![]() ,且cosα=
,且cosα= ![]() ,那么α=
,那么α= ![]() ,故当α=
,故当α= ![]() 时,水渠中水的流失量最小.
时,水渠中水的流失量最小.
【考点精析】解答此题的关键在于理解基本不等式在最值问题中的应用的相关知识,掌握用基本不等式求最值时(积定和最小,和定积最大),要注意满足三个条件“一正、二定、三相等”.

【题目】某种产品的广告费支出x与销售额y(单位:百万元)之间有如下对应数据:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
参考公式:b= 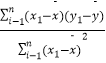 =
= 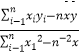 .
.
(1)画出散点图;
(2)求回归直线方程;
(3)试预测广告费支出为10百万元时,销售额多大?