题目内容
【题目】已知向量 
=（1，3）， 
=（3，x）．
（1）如果 ∥ ，求实数x的值；
（2）如果x=﹣1，求向量 与 的夹角．
【答案】
（1）解：向量 
=（1，3）， 
=（3，x），
当 ∥ 时，1×x﹣3×3=0，
解得x=9；
（2）解：当x=﹣1时， =（3，﹣1）；
所以 =1×3+3×（﹣1）=0，
所以cos＜ ， ＞= 
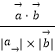=0，
因为＜ ， ＞∈[0，π]，
所以 与 的夹角为 
【解析】（1）根据两向量平行的坐标关系，解得x=9，（2）当x=1时，根据向量的数量积公式可得答案.
【考点精析】本题主要考查了平面向量的坐标运算的相关知识点，需要掌握坐标运算：设
，
则
;
;设
，则
才能正确解答此题．
练习册系列答案
相关题目
【题目】某种产品的广告费支出x与销售额y（单位：百万元）之间有如下对应数据：
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
参考公式：b=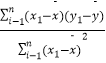 
= 
．
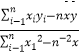（1）画出散点图；
（2）求回归直线方程；
（3）试预测广告费支出为10百万元时，销售额多大？
【题目】假设某种设备使用的年限x（年）与所支出的维修费用y（元）有以下统计资料：
使用年限x | 2 | 3 | 4 | 5 | 6 |
维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
参考数据： 
， 
，
如果由资料知y对x呈线性相关关系．试求：
（1）
；
（2）线性回归方程 
=bx+a．
（3）估计使用10年时，维修费用是多少？
