题目内容
(14分)已知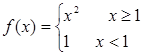
(1)求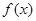 的定义域和值域;
的定义域和值域;
(2)求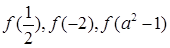 .
.
(1)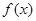 的值域为[1,+∞) ;
的值域为[1,+∞) ;
(2)当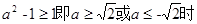
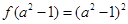 ,
,
当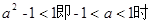 ,
,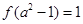 。
。
解析

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
题目内容
(14分)已知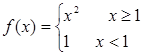
(1)求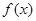 的定义域和值域;
的定义域和值域;
(2)求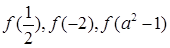 .
.
(1)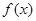 的值域为[1,+∞) ;
的值域为[1,+∞) ;
(2)当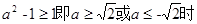
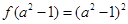 ,
,
当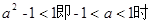 ,
,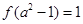 。
。
解析

 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案