题目内容
(本小题满分13分)如图所示,在四棱台 中, 底面ABCD是正方形,且
中, 底面ABCD是正方形,且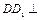 底面
底面 ,
, .
.
(1)求异面直线 与
与 所成角的余弦值;
所成角的余弦值;
(2)试在平面 中确定一个点
中确定一个点 ,使得
,使得 平面
平面 ;
;
(3)在(2)的条件下,求二面角 的余弦值.
的余弦值.
 中, 底面ABCD是正方形,且
中, 底面ABCD是正方形,且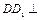 底面
底面 ,
, .
.(1)求异面直线
 与
与 所成角的余弦值;
所成角的余弦值;(2)试在平面
 中确定一个点
中确定一个点 ,使得
,使得 平面
平面 ;
;(3)在(2)的条件下,求二面角
 的余弦值.
的余弦值.
(1)直线AB1与DD1所成角的余弦值为 .
.
(2)略
(3)二面角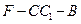 的余弦值为
的余弦值为 .
.
 .
.(2)略
(3)二面角
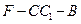 的余弦值为
的余弦值为 .
.解:以D为原点,DA、DC、DD1所在直线为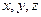 轴,建立如图所示的空间直角坐标系,则D(0,0,0),A(
轴,建立如图所示的空间直角坐标系,则D(0,0,0),A( ),
),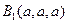 ,
,
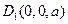 ,
,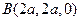 ,
, .
.
(1)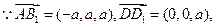
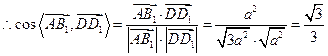 ,
,
即直线AB1与DD1所成角的余弦值为 . …………………(4分)
. …………………(4分)
(2)设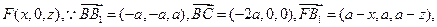
由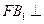 平面
平面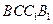 得
得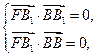 即
即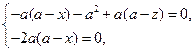 得
得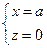
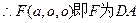 的中点. ………………………………………………(9分)
的中点. ………………………………………………(9分)
(3)由(2)知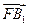 为平面
为平面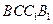 的法向量.
的法向量.
设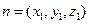 为平面
为平面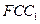 的法向量,
的法向量,
 .
.
由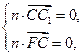 即
即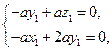
令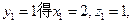
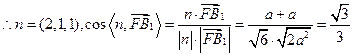 ,
,
即二面角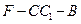 的余弦值为
的余弦值为 . …………………………………(13分)
. …………………………………(13分)
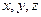 轴,建立如图所示的空间直角坐标系,则D(0,0,0),A(
轴,建立如图所示的空间直角坐标系,则D(0,0,0),A( ),
),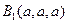 ,
,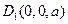 ,
,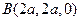 ,
, .
.(1)
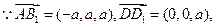
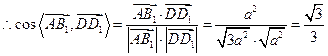 ,
,即直线AB1与DD1所成角的余弦值为
 . …………………(4分)
. …………………(4分)(2)设
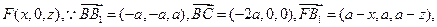
由
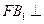 平面
平面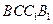 得
得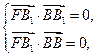 即
即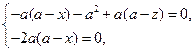 得
得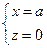
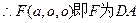 的中点. ………………………………………………(9分)
的中点. ………………………………………………(9分)(3)由(2)知
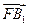 为平面
为平面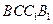 的法向量.
的法向量.设
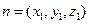 为平面
为平面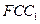 的法向量,
的法向量, .
.由
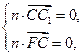 即
即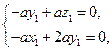
令
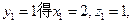
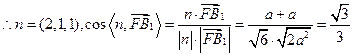 ,
,即二面角
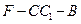 的余弦值为
的余弦值为 . …………………………………(13分)
. …………………………………(13分)
练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目



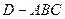 中,已知△
中,已知△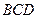 是正三角形,
是正三角形,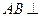 平面
平面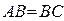 ,
,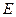 为
为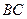 的中点,
的中点,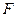 在棱
在棱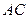 上,且
上,且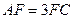 ,
, 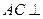 平面
平面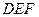 ;
;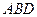 所成的锐二面角的余弦值;
所成的锐二面角的余弦值; 为
为 的中点,问
的中点,问 ,使
,使 平面
平面

 是⊙
是⊙ 的切线,
的切线,  为切点,
为切点,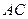 是⊙O的割线,与⊙
是⊙O的割线,与⊙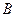 ,
,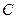 两点,圆心
两点,圆心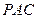 的内部,点
的内部,点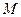 是
是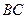 的中点.
的中点.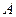 ,
,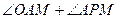 的大小.
的大小.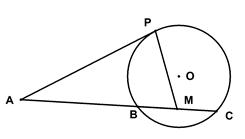
 为正三角形,
为正三角形, 平面ABC,AD//BE,且BE=AB+2AD,P是EC的中点。
平面ABC,AD//BE,且BE=AB+2AD,P是EC的中点。 平面PBD。
平面PBD。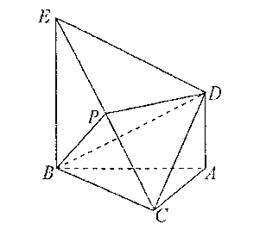
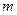 、
、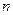 与平面
与平面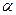 、
、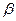 ,有下列四个命题:
,有下列四个命题: 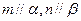 且
且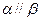 ,则
,则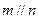 ; ②
; ②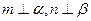 且
且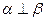 ,则
,则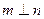 ;
;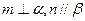 且
且 且
且