题目内容
(本题满分14分)
如图,四棱锥P—ABCD的底面ABCD为一直角梯形,其中BA⊥AD,CD⊥AD,CD=AD=2AB,PA⊥底面ABCD,E是PC的中点.
(Ⅰ)求证:BE//平面PAD;
(Ⅱ)若BE⊥平面PCD。
(i)求异面直线PD与BC所成角的余弦值;
(ii)求二面角E—BD—C的余弦值.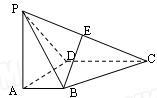
如图,四棱锥P—ABCD的底面ABCD为一直角梯形,其中BA⊥AD,CD⊥AD,CD=AD=2AB,PA⊥底面ABCD,E是PC的中点.
(Ⅰ)求证:BE//平面PAD;
(Ⅱ)若BE⊥平面PCD。
(i)求异面直线PD与BC所成角的余弦值;
(ii)求二面角E—BD—C的余弦值.

(Ⅰ)略
(Ⅱ)(i)异面直线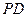 与
与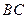 所成角的余弦值为
所成角的余弦值为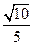
(ii)二面角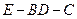 的余弦值为
的余弦值为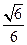
(Ⅱ)(i)异面直线
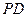 与
与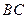 所成角的余弦值为
所成角的余弦值为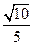
(ii)二面角
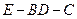 的余弦值为
的余弦值为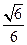
设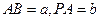 ,建立如图的空间坐标系,
,建立如图的空间坐标系,
 ,
, ,
,
 ,
,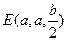 .……………………………………2分
.……………………………………2分
(Ⅰ)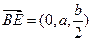 ,
,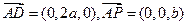 ,
,
所以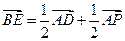 ,
,
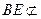 平面
平面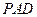 ,
, 平面
平面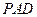 . ……………………………………4分
. ……………………………………4分
(Ⅱ)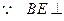 平面
平面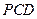 ,
,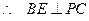 ,即
,即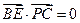
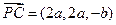 ,
,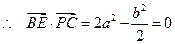 ,即
,即 .…………………6分
.…………………6分
① ,
,
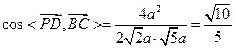 ,
,
所以异面直线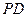 与
与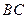 所成角的余弦值为
所成角的余弦值为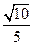 ……………………………10分
……………………………10分
②平面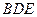 和平面
和平面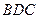 中,
中,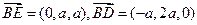
 ,
,
所以平面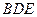 的一个法向量为
的一个法向量为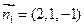 ;
;
平面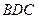 的一个法向量为
的一个法向量为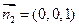 ;……………………………………12分
;……………………………………12分
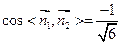 ,所以二面角
,所以二面角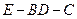 的余弦值为
的余弦值为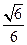 …………………14分
…………………14分
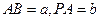 ,建立如图的空间坐标系,
,建立如图的空间坐标系, ,
, ,
, ,
,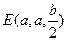 .……………………………………2分
.……………………………………2分(Ⅰ)
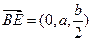 ,
,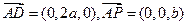 ,
,所以
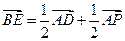 ,
, 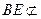 平面
平面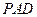 ,
, 平面
平面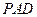 . ……………………………………4分
. ……………………………………4分(Ⅱ)
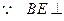 平面
平面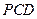 ,
,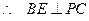 ,即
,即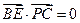
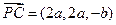 ,
,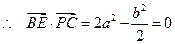 ,即
,即 .…………………6分
.…………………6分①
 ,
,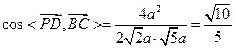 ,
,所以异面直线
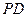 与
与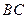 所成角的余弦值为
所成角的余弦值为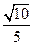 ……………………………10分
……………………………10分②平面
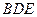 和平面
和平面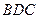 中,
中,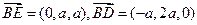
 ,
,所以平面
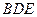 的一个法向量为
的一个法向量为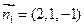 ;
; 平面
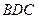 的一个法向量为
的一个法向量为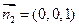 ;……………………………………12分
;……………………………………12分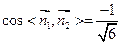 ,所以二面角
,所以二面角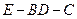 的余弦值为
的余弦值为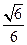 …………………14分
…………………14分
练习册系列答案
相关题目
 底面ABCD,PA=AB=
底面ABCD,PA=AB=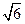 ,点E是棱PB的中点。(1)求直线AD与平面PBC的距离。
,点E是棱PB的中点。(1)求直线AD与平面PBC的距离。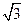 ,求二面角A-EC-D的平面角的余弦值。
,求二面角A-EC-D的平面角的余弦值。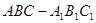 中,
中,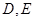 分别为
分别为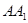 ,
,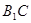 的中点.
的中点.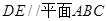 ;
; 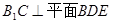 .
.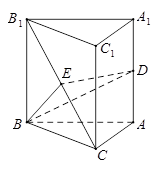

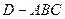 中,已知△
中,已知△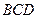 是正三角形,
是正三角形,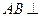 平面
平面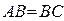 ,
,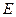 为
为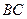 的中点,
的中点,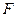 在棱
在棱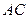 上,且
上,且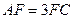 ,
, 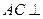 平面
平面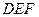 ;
;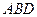 所成的锐二面角的余弦值;
所成的锐二面角的余弦值;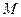 为
为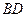 的中点,问
的中点,问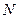 ,使
,使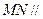 平面
平面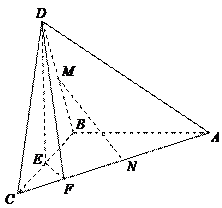
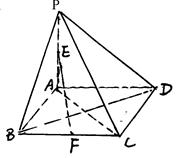
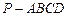 中,底面ABCD为菱形,
中,底面ABCD为菱形,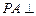 底面
底面 ,
, 为
为 的中点,
的中点, 为
为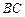 的中点,求证:
的中点,求证: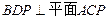 ;
; .
.

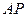 是⊙
是⊙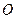 的切线,
的切线, 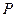 为切点,
为切点,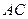 是⊙O的割线,与⊙
是⊙O的割线,与⊙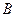 ,
,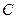 两点,圆心
两点,圆心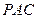 的内部,点
的内部,点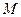 是
是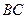 的中点.
的中点. ,
,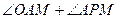 的大小.
的大小.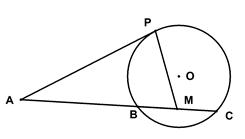
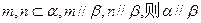 .
.