题目内容
15.定义运算a?b为执行如右图所示的程序框图输出的S值,则$({2^-}^{{{log}_2}3})?({log_{\frac{1}{2}}}4)$的值为( )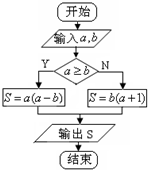
| A. | $\frac{7}{9}$ | B. | $-\frac{8}{3}$ | C. | 4 | D. | -4 |
分析 由已知的程序框图可知:本程序的功能是:计算并输出分段函数S=$\left\{\begin{array}{l}{a(a-b)}&{a≥b}\\{b(a+1)}&{a<b}\end{array}\right.$的值,由已知计算出a,b的值,代入可得答案.
解答 解:由已知的程序框图可知:
本程序的功能是:计算并输出分段函数S=$\left\{\begin{array}{l}{a(a-b)}&{a≥b}\\{b(a+1)}&{a<b}\end{array}\right.$的值
∵a=${2}^{{-log}_{2}^{3}}$=$\frac{1}{3}$>b=${log}_{\frac{1}{2}}^{4}$=-2,
∴S=$\frac{1}{3}$×($\frac{1}{3}$+2)=$\frac{7}{9}$.
故选:A.
点评 本题考查的知识点是程序框图,其中根据已知的程序框图分析出程序的功能是解答的关键,属于基础题.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
6.在△ABC中,a,b,c分别为角A,B,C所对的边,若acosA=bcosB,则此三角形一定是( )
| A. | 等腰直角三角形 | B. | 等腰或直角三角形 | ||
| C. | 等腰三角形 | D. | 直角三角形 |
10.函数f(x)=ax+loga(x+1)在[0,1]上的最大值与最小值之和为a,则a的值为( )
| A. | $\frac{1}{4}$ | B. | 4 | C. | $\frac{1}{2}$ | D. | 2 |
7.已知f(x)=cosx,且f1(x)=f′(x),fn+1(x)=fn′(x)(n∈N*),则f2015(x)=( )
| A. | -sin x | B. | -cos x | C. | sin x | D. | cos x |
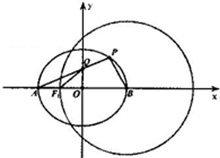 如图,点A,B分别是椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点,圆B:(x-2)2+y2=9,经过椭圆E的左焦点F.
如图,点A,B分别是椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点,圆B:(x-2)2+y2=9,经过椭圆E的左焦点F.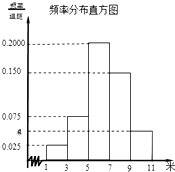 为了解某校今年高一年级女生的身体素质状况,从该校高一年级女生中抽取了一部分学生进行“掷铅球”的项目测试,成绩低于5米为不合格,成绩在5至7米(含5米不含7米)的为及格,成绩在7米至11米(含7米和11米,假定该校高一女生掷铅球均不超过11米)为优秀.把获得的所有数据,分成[1,3),[3,5),[5,7),[7,9),[9,11]五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在9米到11米之间.
为了解某校今年高一年级女生的身体素质状况,从该校高一年级女生中抽取了一部分学生进行“掷铅球”的项目测试,成绩低于5米为不合格,成绩在5至7米(含5米不含7米)的为及格,成绩在7米至11米(含7米和11米,假定该校高一女生掷铅球均不超过11米)为优秀.把获得的所有数据,分成[1,3),[3,5),[5,7),[7,9),[9,11]五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在9米到11米之间.