题目内容
10.函数f(x)=ax+loga(x+1)在[0,1]上的最大值与最小值之和为a,则a的值为( )| A. | $\frac{1}{4}$ | B. | 4 | C. | $\frac{1}{2}$ | D. | 2 |
分析 由题意可判断函数f(x)=ax+loga(x+1)在[0,1]上单调,从而可得f(0)+f(1)=a,从而解得.
解答 解:∵函数f(x)=ax+loga(x+1)在[0,1]上单调,
∴函数f(x)=ax+loga(x+1)在[0,1]上的最大值与最小值在x=0与x=1时取得;
∴f(0)+f(1)=a,
即1+0+a+loga2=a,
即loga2=-1,
即a=$\frac{1}{2}$;
故选:C.
点评 本题考查了对数函数与指数函数的单调性的判断与应用,同时考查了最值的应用,属于基础题.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
5.下列函数中,既是偶函数,又是区间(0,+∞)内的减函数的是( )
| A. | y=log2x2 | B. | y=cosx | C. | y=-2|x| | D. | y=2-x |
15.定义运算a?b为执行如右图所示的程序框图输出的S值,则$({2^-}^{{{log}_2}3})?({log_{\frac{1}{2}}}4)$的值为( )
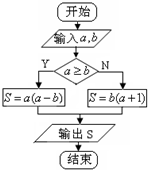

| A. | $\frac{7}{9}$ | B. | $-\frac{8}{3}$ | C. | 4 | D. | -4 |
19.已知a为常数,y=|x-a|-|x+a|最大值为M,最小值为N,且M-N=12,则实数a的值为( )
| A. | 6 | B. | ±6 | C. | 3 | D. | ±3 |