题目内容
7.已知f(x)=cosx,且f1(x)=f′(x),fn+1(x)=fn′(x)(n∈N*),则f2015(x)=( )| A. | -sin x | B. | -cos x | C. | sin x | D. | cos x |
分析 由题意对函数的变化规律进行探究,发现呈周期性的变化,且其周期是4,即可得到结论
解答 解:由题意f(x)=cosx,
f1(x)=f′(x)=-sinx,
f2(x)=f1′(x)=-cosx,
f3(x)=f2′(x)=sinx,
f4(x)=f3′(x)=cosx,
由此可知,在逐次求导的过程中,所得的函数呈周期性变化,从0开始计,周期是4,
∵2015=4×503+3,
故f2015(x)=f3(x)=sinx,
故选:C.
点评 本题考查函数的周期性,探究过程中用的是归纳推理,对其前几项进行研究得出规律,求解本题的关键一是要归纳推理的意识,一是对正、余弦函数的导数求法公式熟练掌握.

练习册系列答案
相关题目
15.定义运算a?b为执行如右图所示的程序框图输出的S值,则$({2^-}^{{{log}_2}3})?({log_{\frac{1}{2}}}4)$的值为( )
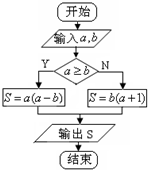

| A. | $\frac{7}{9}$ | B. | $-\frac{8}{3}$ | C. | 4 | D. | -4 |
19.已知a为常数,y=|x-a|-|x+a|最大值为M,最小值为N,且M-N=12,则实数a的值为( )
| A. | 6 | B. | ±6 | C. | 3 | D. | ±3 |