Question

已知以点C（1，﹣2）为圆心的圆与直线x+y﹣1=0相切．
（1）求圆C的标准方程；
（2）求过圆内一点P（2，﹣）的最短弦所在直线的方程．

Answer 1

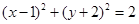（1）；（2）.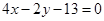

解析试题分析：
解题思路：（1）因为圆与直线x+y﹣1=0相切，所以利用点到直线的距离公式求出圆心到直线的距离即为圆的半径，写出圆的标准方程即可；（2）先判定过P点的最短弦所在直线与过P点的直径垂直，再进行求解.
规律总结：直线圆的位置关系，主要涉及直线与圆相切、相交、相离，在解决直线圆的位置关系时，要注意结合初中平面几何中的直线与圆的知识.
试题解析：（1）圆的半径r=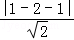=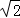，所以圆的方程为（x﹣1）²+（y+2）²=2．
圆的圆心坐标为C（1，﹣2），则过P点的直径所在直线的斜率为﹣，
由于过P点的最短弦所在直线与过P点的直径垂直，
∴过P点的最短弦所在直线的斜率为2，
∴过P点的最短弦所在直线的方程y+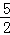=2（x﹣2），即4x﹣2y﹣13=0.
考点：1.圆的标准方程；2.直线与圆的位置关系.