题目内容
已知直线 ,圆
,圆 .
.
(1)求直线 被圆
被圆 所截得的弦长;
所截得的弦长;
(2)如果过点 的直线
的直线 与直线
与直线 垂直,
垂直, 与圆心在直线
与圆心在直线 上的圆
上的圆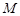 相切,圆
相切,圆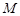 被直线
被直线 分成两段圆弧,且弧长之比为
分成两段圆弧,且弧长之比为 ,求圆
,求圆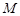 的方程.
的方程.
(1)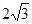 ;(2)
;(2)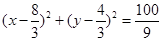 或
或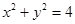 .
.
解析试题分析:(1)由题意可以通过求弦心距进而求得弦长,而弦心距即为圆心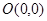 到直线
到直线 的距离:
的距离: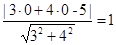 ,再由垂径定理,弦长为
,再由垂径定理,弦长为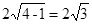 ;(2)根据题意可求得
;(2)根据题意可求得 :
: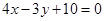 ,由圆心
,由圆心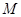 在直线
在直线 上,可设
上,可设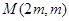 ,从而根据
,从而根据 与圆
与圆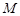 相切可知圆
相切可知圆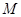 的半径
的半径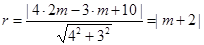 ,再由圆
,再由圆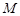 被直线
被直线 分成两段圆弧,且弧长之比为
分成两段圆弧,且弧长之比为 ,可知两段弧的度数分为为
,可知两段弧的度数分为为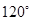 ,
,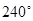 ,从而直线
,从而直线 截圆
截圆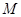 的弦的弦心距为半径的一半,即有关于
的弦的弦心距为半径的一半,即有关于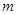 的方程:
的方程: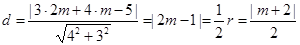 ,解得
,解得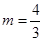 或
或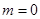 ,从而可得圆
,从而可得圆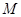 的方程为:
的方程为: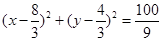 或
或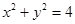 .
.
试题解析:(1)直线 被圆
被圆 所截得弦弦心距为
所截得弦弦心距为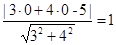 ,∴弦长为
,∴弦长为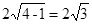 ; 3分
; 3分
∵ 过点
过点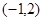 且与
且与 垂直,∴
垂直,∴ :
: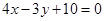 , 3分
, 3分
∵圆心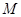 在直线
在直线 上,∴设
上,∴设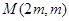 ,∵
,∵ 与圆
与圆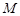 相切,∴
相切,∴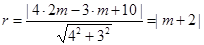 ,
,
设 与圆
与圆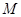 交于
交于 ,
, 两点,∵圆
两点,∵圆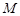 被直线
被直线 分成两段圆弧,且弧长之比为
分成两段圆弧,且弧长之比为 ,∴
,∴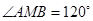 ,
,
即可得 的弦心距
的弦心距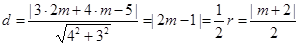 ,解得
,解得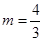 或
或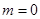 ,
,
∴圆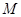 的方程为:
的方程为: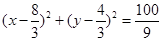 或
或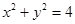 . 6分
. 6分
考点:1.直线与圆的位置关系;2.圆的标准方程.

练习册系列答案
相关题目
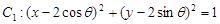 与圆
与圆 ,在下列说法中:
,在下列说法中: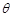 ,圆
,圆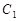 与圆
与圆 始终相切;
始终相切;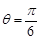 时,圆
时,圆 截得的弦长为
截得的弦长为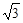 ;
;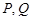 分别为圆
分别为圆 的最大值为4.
的最大值为4. )的最短弦所在直线的方程.
)的最短弦所在直线的方程. 与圆C:
与圆C: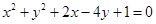 的两个交点,并且面积有最小值,求此圆的方程.
的两个交点,并且面积有最小值,求此圆的方程. 相切,且圆心C在直线
相切,且圆心C在直线 上.
上. 的直线l与圆C相交于A,B两点, 且
的直线l与圆C相交于A,B两点, 且 , 求直线l的方程.
, 求直线l的方程.
 (
( )
) 时,求经过原点且与圆
时,求经过原点且与圆 相切的直线
相切的直线 的方程;
的方程; 的内部,求实数
的内部,求实数 的取值范围.
的取值范围. 的方程:
的方程:
 相交于
相交于 ,
, 两点,且
两点,且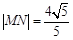 ,求
,求 的值
的值