Question

【题目】已知椭圆的两焦点为， ， 为椭圆上一点，且到两个焦点的距离之和为6．

（1）求椭圆的标准方程；

（2）若已知直线，当为何值时，直线与椭圆有公共点？

（3）若，求的面积．

Answer 1

【答案】（1）；（2）；（3）7．

【解析】试题分析:(1)由焦点坐标得到c,由椭圆的定义求出a,进而求出b的值,即可得出椭圆的方程;(2)联立直线与椭圆方程,消去y, 直线与椭圆有公共点即所得一元二次方程有解,计算得出m的范围;(3) 中， ，由勾股定理有,结合椭圆的定义代入化简可得,根据三角形的面积公式求解即可.

试题解析:

（1）∵椭圆的焦点是和，椭圆上一点到两个焦点的距离之和为6，

∴设所求的椭圆方程为，

∴依题意有， ，∴，

∴所求的椭圆方程为．

（2）由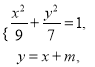得，

由得，则，

∴当时，直线与椭圆有公共点．

（3）∵点是椭圆上一点，

∴由椭圆定义有，①

又中， ，

∴由勾股定理有，即，②

①2 ②，得，

∴．