Question

【题目】已知y=f（x）是定义在R上的偶函数，当x≥0时，f（x）=x2﹣2x．
（1）求f（x）的解析式；
（2）作出函数f（x）的图象，并指出其单调区间．（不需要严格证明）

Answer 1

【答案】
（1）解：∵y=f（x）是定义在R上的偶函数，当x≥0时，f（x）=x2﹣2x，

当x＜0时，﹣x＞0，

f（﹣x）=（﹣x）2﹣2（﹣x）=x2+2x，

∴f（x）=f（﹣x）=x2+2x，

∴f（x）=

（2）解：∵f（x）= ，

∴当x≥0时，y=x2﹣2x，抛物线开口向上，对称轴方程为x=1，顶点坐标（1，﹣1），

当y=0时，x1=0，x2=2；当x=0时，y=0．

当x＜0时，y=x2+2x，抛物线开口向上，对称轴方程为x=﹣1，顶点坐标（﹣1，﹣1），

当y=0时，x=﹣2．

由此能作出函数f（x）的图象如下：

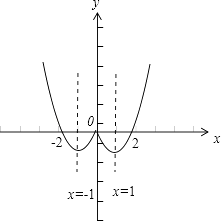
结合图象，知f（x）的增区间是（﹣1，0），（1，+∞）；减区间是（﹣∞，﹣1），（0，1）

【解析】（1）由y=f（x）是定义在R上的偶函数，当x≥0时，f（x）=x2﹣2x，知当x＜0时，f（x）=f（﹣x）=x2+2x，由此能求出f（x）的解析式．（2）当x≥0时，y=x2﹣2x，抛物线开口向上，对称轴方程为x=1，顶点坐标（1，﹣1），当y=0时，x1=0，x2=2；当x=0时，y=0；当x＜0时，y=x2+2x，抛物线开口向上，对称轴方程为x=﹣1，顶点坐标（﹣1，﹣1），当y=0时，x=﹣2．由此能作出函数f（x）的图象．结合图象，能求出f（x）的单调区间．
【考点精析】利用奇偶性与单调性的综合对题目进行判断即可得到答案，需要熟知奇函数在关于原点对称的区间上有相同的单调性；偶函数在关于原点对称的区间上有相反的单调性．