题目内容
(本小题满分14分)已知区域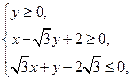 的外接圆C与x轴交于点A1、A2,椭圆C1以线段A1A2为长轴,离心率
的外接圆C与x轴交于点A1、A2,椭圆C1以线段A1A2为长轴,离心率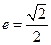 .
.
⑴求圆C及椭圆C1的方程;
⑵设圆 与
与 轴正半轴交于点D,
轴正半轴交于点D,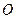 点为坐标原点,
点为坐标原点,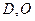 中点为
中点为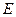 ,问是否存在直线
,问是否存在直线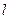 与椭圆
与椭圆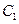 交于
交于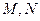 两点,且
两点,且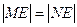 ?若存在,求出直线
?若存在,求出直线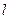 与
与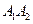 夹角
夹角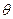 的正切值的取值范围;若不存在,请说明理由.
的正切值的取值范围;若不存在,请说明理由.
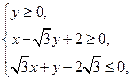 的外接圆C与x轴交于点A1、A2,椭圆C1以线段A1A2为长轴,离心率
的外接圆C与x轴交于点A1、A2,椭圆C1以线段A1A2为长轴,离心率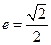 .
.⑴求圆C及椭圆C1的方程;
⑵设圆
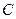 与
与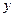 轴正半轴交于点D,
轴正半轴交于点D,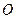 点为坐标原点,
点为坐标原点,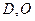 中点为
中点为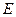 ,问是否存在直线
,问是否存在直线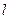 与椭圆
与椭圆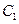 交于
交于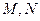 两点,且
两点,且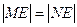 ?若存在,求出直线
?若存在,求出直线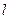 与
与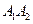 夹角
夹角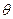 的正切值的取值范围;若不存在,请说明理由.
的正切值的取值范围;若不存在,请说明理由. ,
,

解:⑴由题意可知,区域是以 及点
及点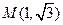 为顶点的三角形,
为顶点的三角形,
∵ ,∴
,∴ 为直角三角形. ……2分
为直角三角形. ……2分
∴外接圆C以原点O为圆心,线段A1A2为直径,故其方程为 .
.
∵2a=4,∴a=2.
又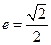 ,∴
,∴ ,可得
,可得 .
.
∴所求椭圆C1的方程是 . ……6分
. ……6分
⑵点 坐标为
坐标为 ,故点
,故点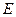 坐标为
坐标为 ,显然
,显然 可满足要求;
可满足要求; 时不满足题意. ……8分
时不满足题意. ……8分
当 时,设
时,设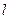 的方程为
的方程为 ,
,
由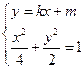 ,得
,得 ,
,
由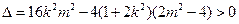 ,得
,得 ; ……10分
; ……10分
设 ,
, 的中点为
的中点为 ,
,
则 .
.
 ,即
,即 ,解得
,解得 .
.
……12分
 ,得
,得 .
.
综上,直线 与
与 夹角
夹角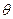 的正切值的取值范围是
的正切值的取值范围是 . ……14分
. ……14分
 及点
及点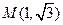 为顶点的三角形,
为顶点的三角形,∵
 ,∴
,∴ 为直角三角形. ……2分
为直角三角形. ……2分∴外接圆C以原点O为圆心,线段A1A2为直径,故其方程为
 .
.∵2a=4,∴a=2.
又
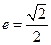 ,∴
,∴ ,可得
,可得 .
.∴所求椭圆C1的方程是
 . ……6分
. ……6分⑵点
 坐标为
坐标为 ,故点
,故点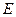 坐标为
坐标为 ,显然
,显然 可满足要求;
可满足要求; 时不满足题意. ……8分
时不满足题意. ……8分当
 时,设
时,设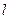 的方程为
的方程为 ,
,由
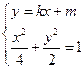 ,得
,得 ,
,由
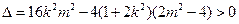 ,得
,得 ; ……10分
; ……10分设
 ,
, 的中点为
的中点为 ,
,则
 .
. ,即
,即 ,解得
,解得 .
.……12分
 ,得
,得 .
.综上,直线
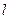 与
与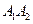 夹角
夹角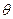 的正切值的取值范围是
的正切值的取值范围是 . ……14分
. ……14分
练习册系列答案
 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 ,(
,( )的一个焦点,且这条准线与双曲线的两个焦点连线互相垂直,又抛 物线与双曲线交于点
)的一个焦点,且这条准线与双曲线的两个焦点连线互相垂直,又抛 物线与双曲线交于点 ,求抛物线和双曲线的方程.
,求抛物线和双曲线的方程.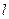 :
: 过抛物线
过抛物线 的焦点.
的焦点. ,若
,若 ,矩阵阵
,矩阵阵 ,
, ,求在矩阵
,求在矩阵 作用下变换所得到的图形的面积.
作用下变换所得到的图形的面积.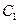 :
: 经过椭圆
经过椭圆 :
: 的两个焦点.
的两个焦点.
 ,又
,又 为
为 轴上的两个交点,若
轴上的两个交点,若 的重心在抛物线
的重心在抛物线 关于直线
关于直线 对称的曲线方程是( )
对称的曲线方程是( )



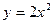 ,点
,点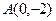 及点
及点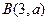 ,从A点观察点B,要使视线不被曲线C挡住,则实数a的取值范围是( )
,从A点观察点B,要使视线不被曲线C挡住,则实数a的取值范围是( )



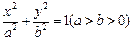 与抛物线
与抛物线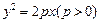 有相同的焦点
有相同的焦点 ,
, 是椭圆与抛物线的的交点,若
是椭圆与抛物线的的交点,若 经过焦点
经过焦点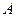 、
、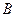 为抛物线
为抛物线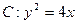 上的不同两点,
上的不同两点,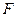 为抛物线
为抛物线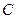 的焦点,若
的焦点,若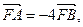 则直线
则直线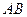 的斜率为( )
的斜率为( )


