题目内容
已知抛物线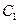 :
: 经过椭圆
经过椭圆 :
: 的两个焦点.
的两个焦点.

(1) 求椭圆 的离心率;
的离心率;
(2) 设 ,又
,又 为
为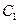 与
与 不在
不在 轴上的两个交点,若
轴上的两个交点,若 的重心在抛物线
的重心在抛物线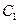 上,求
上,求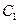 和
和 的方程.
的方程.
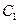 :
: 经过椭圆
经过椭圆 :
: 的两个焦点.
的两个焦点.
(1) 求椭圆
 的离心率;
的离心率;(2) 设
 ,又
,又 为
为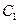 与
与 不在
不在 轴上的两个交点,若
轴上的两个交点,若 的重心在抛物线
的重心在抛物线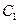 上,求
上,求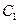 和
和 的方程.
的方程.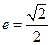
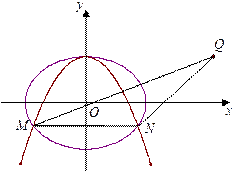
抛物线
 的方程为:
的方程为: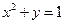 ,
,椭圆
 的方程为:
的方程为: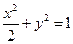 .
.考查椭圆和抛物线的定义、基本量,通过交点三角形来确认方程。
解:(1)因为抛物线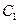 经过椭圆
经过椭圆 的两个焦点
的两个焦点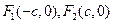 ,
,
所以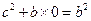 ,即
,即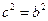 ,由
,由 得椭圆
得椭圆 的离心率
的离心率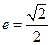 .
.
(2)由(1)可知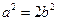 ,椭圆
,椭圆 的方程为:
的方程为:
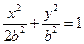
联立抛物线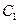 的方程
的方程 得:
得: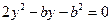 ,
,
解得: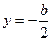 或
或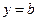 (舍去),所以
(舍去),所以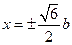 ,
,
即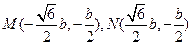 ,所以
,所以 的重心坐标为
的重心坐标为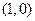 .
.
因为重心在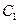 上,所以
上,所以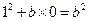 ,得
,得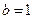 .所以
.所以 .
.
所以抛物线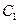 的方程为:
的方程为: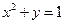 ,
,
椭圆 的方程为:
的方程为: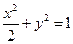 .
.
解:(1)因为抛物线
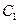 经过椭圆
经过椭圆 的两个焦点
的两个焦点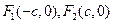 ,
,所以
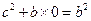 ,即
,即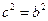 ,由
,由 得椭圆
得椭圆 的离心率
的离心率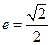 .
.(2)由(1)可知
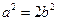 ,椭圆
,椭圆 的方程为:
的方程为: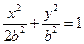
联立抛物线
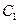 的方程
的方程 得:
得: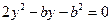 ,
,解得:
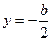 或
或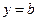 (舍去),所以
(舍去),所以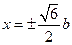 ,
,即
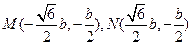 ,所以
,所以 的重心坐标为
的重心坐标为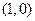 .
.因为重心在
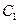 上,所以
上,所以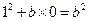 ,得
,得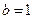 .所以
.所以 .
.所以抛物线
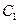 的方程为:
的方程为: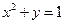 ,
,椭圆
 的方程为:
的方程为: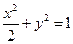 .
.
练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
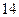 分)
分)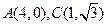 ,点M是OA的中点,点P在线段BC上运动(包括端点),如图
,点M是OA的中点,点P在线段BC上运动(包括端点),如图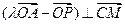 ?若存在,求出满足条件的实数λ的取值范围;若不存在,请说明理由。
?若存在,求出满足条件的实数λ的取值范围;若不存在,请说明理由。
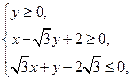 的外接圆C与x轴交于点A1、A2,椭圆C1以线段A1A2为长轴,离心率
的外接圆C与x轴交于点A1、A2,椭圆C1以线段A1A2为长轴,离心率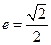 .
.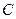 与
与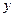 轴正半轴交于点D,
轴正半轴交于点D,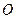 点为坐标原点,
点为坐标原点,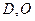 中点为
中点为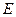 ,问是否存在直线
,问是否存在直线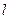 与椭圆
与椭圆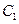 交于
交于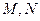 两点,且
两点,且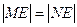 ?若存在,求出直线
?若存在,求出直线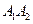 夹角
夹角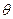 的正切值的取值范围;若不存在,请说明理由.
的正切值的取值范围;若不存在,请说明理由. ,若按向量
,若按向量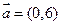 作平移变换得曲线
作平移变换得曲线 ;若将曲线
;若将曲线 按伸缩系数
按伸缩系数 向着
向着 轴作伸缩变换,再按伸缩系数3向着
轴作伸缩变换,再按伸缩系数3向着 轴作伸缩变换得到曲线
轴作伸缩变换得到曲线
 为
为 为
为 与曲线
与曲线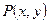 (
( )到定点
)到定点 的距离与到
的距离与到 轴的距离之差为
轴的距离之差为 .
. 的轨迹
的轨迹 的方程;
的方程; ,
, 为
为 ,求证:直线
,求证:直线 必过一定
必过一定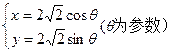 交
交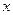 轴于A、B两点,曲线C是以AB为长轴,离心率
轴于A、B两点,曲线C是以AB为长轴,离心率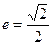 的椭圆。
的椭圆。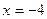 上的任一点,以OM为直径的圆交曲线D于P,Q两点(O为坐标原点)。若直线PQ与椭圆C交于G,H两点,交x轴于点E,且
上的任一点,以OM为直径的圆交曲线D于P,Q两点(O为坐标原点)。若直线PQ与椭圆C交于G,H两点,交x轴于点E,且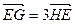 。试求此时弦PQ的长。
。试求此时弦PQ的长。 的距离比它到直线
的距离比它到直线 的距离小2,则点P的轨迹方程是 .
的距离小2,则点P的轨迹方程是 .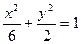 和双曲线
和双曲线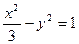 的公共焦点为
的公共焦点为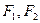 ,
,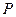 是两曲线的一个公共点,则cos
是两曲线的一个公共点,则cos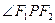 的值等于( )
的值等于( )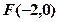 ,则该抛物线的准线方程为 ( )
,则该抛物线的准线方程为 ( )


