题目内容
已知椭圆C的焦点为F1(-1,0)、F2(1,0),点P(-1,
)在椭圆上.
(1)求椭圆C的方程;
(2)若抛物线E:y2=2px(p>0)与椭圆C相交于点M、N,当△OMN(O是坐标原点)的面积取得最大值时,求P的值.
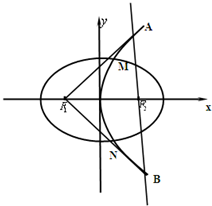
(3)在(2)的条件下,过点F2作任意直线l与抛物线E相交于点A、B两点,则直线AF1与直线BF1的斜率之和是否为定值?若是,求出定值;若不是,说明理由.
| ||
| 2 |
(1)求椭圆C的方程;
(2)若抛物线E:y2=2px(p>0)与椭圆C相交于点M、N,当△OMN(O是坐标原点)的面积取得最大值时,求P的值.
(3)在(2)的条件下,过点F2作任意直线l与抛物线E相交于点A、B两点,则直线AF1与直线BF1的斜率之和是否为定值?若是,求出定值;若不是,说明理由.

(1)依题意,设椭圆C的方程为
+
=1,…(1分),
∵椭圆C的焦点为F1(-1,0)、F2(1,0),点P(-1,
)在椭圆上,
∴2a=|PF1|+|PF2|=
+
=2
,…(2分),
∴a=
,c=1,…(3分),
∴b=
=1,…(4分),
∴椭圆C的方程为
+y2=1.…(4分)
(2)根据椭圆和抛物线的对称性,
设M(x0,y0)、N(x0,-x0),(x0,y0>0)…(5分),
△OMN的面积S=
x0•(2y0)=x0y0,…(6分),
∵M(x0,y0)在椭圆上,∴
+y02=1,∴y02=1-
,
那么S2=x02y02=x02(1-
)=-
(x02-1)2+
,
当x02=1时,Smax2=
,
即当x0=1,(x0>1)时,Smax=
.
将x0=1代入y02=1-
得
,…(8分),
∵M(1,
)在抛物线y2=2px上,∴
=2p,
解得p=
.…(9分),
(3)(A)当直线l垂直于x轴时,
根据抛物线的对称性,有∠AF1F2=∠BF1F2,
则kAF2+kBF1=0.…(10分),
(B)当直线l与x轴不垂直时,
依题意设直线l的方程为y=k(x-1),k≠0,
A(x1,y1),B(x2,y2),则A,B两点的坐标满足方程组
.…(11分),
化简得2k2x2-(4k2+1)x+2k2=0,
依韦达定理得
,…(12分),
又kAF1=
=
,yBF1=
,
∴kAF1+kAF1=
+
=
=
,
把
代入,得kAF1+kBF1=0,
综上,直线AF1与直线BF1的斜率之和为定值0.…(14分),
| x2 |
| a2 |
| y2 |
| b2 |
∵椭圆C的焦点为F1(-1,0)、F2(1,0),点P(-1,
| ||
| 2 |
∴2a=|PF1|+|PF2|=
0+(
|
4+(
|
| 2 |
∴a=
| 2 |
∴b=
| a2-b2 |
∴椭圆C的方程为
| x2 |
| 2 |
(2)根据椭圆和抛物线的对称性,
设M(x0,y0)、N(x0,-x0),(x0,y0>0)…(5分),
△OMN的面积S=
| 1 |
| 2 |
∵M(x0,y0)在椭圆上,∴
| x02 |
| 2 |
| x02 |
| 2 |
那么S2=x02y02=x02(1-
| x02 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当x02=1时,Smax2=
| 1 |
| 2 |
即当x0=1,(x0>1)时,Smax=
| ||
| 2 |
将x0=1代入y02=1-
| x02 |
| 2 |
|
∵M(1,
| ||
| 2 |
| 1 |
| 2 |
解得p=
| 1 |
| 4 |
(3)(A)当直线l垂直于x轴时,
根据抛物线的对称性,有∠AF1F2=∠BF1F2,
则kAF2+kBF1=0.…(10分),
(B)当直线l与x轴不垂直时,
依题意设直线l的方程为y=k(x-1),k≠0,
A(x1,y1),B(x2,y2),则A,B两点的坐标满足方程组
|
化简得2k2x2-(4k2+1)x+2k2=0,
依韦达定理得
|
又kAF1=
| y1 |
| x1+1 |
| k(x1-1) |
| x1+1 |
| k(x2-1) |
| x2+1 |
∴kAF1+kAF1=
| k(x1-1) |
| x1+1 |
| k(x2-1) |
| x2+1 |
=
| k(x1-1)(x2+1)+k(x2-1)(x1+1) |
| (x1+1)(x2+1) |
=
| 2k(x1x2-1) |
| (x1+1)(x2+1) |
把
|
综上,直线AF1与直线BF1的斜率之和为定值0.…(14分),

练习册系列答案
相关题目