题目内容

已知椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)经过点A（2，1），离心率为
2
2
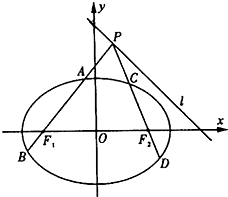
．过点B（3，0）的直线l与椭圆C交于不同的两点M，N．
（Ⅰ）求椭圆C的方程；
（Ⅱ）求
BM
•
BN
的取值范围；
（Ⅲ）设直线AM和直线AN的斜率分别为kAM和kAN，求证：kAM+kAN为定值．
（Ⅰ）由题意得
4
a2
+
1
b2
=1
a2=b2+c2
c
a
=
2
2
.
，解得a=
6
，b=
3
．故椭圆C的方程为
x2
6
+
y2
3
=1．
（Ⅱ）由题意显然直线l的斜率存在，设直线l方程为y=k（x-3），
由
y=k(x-3)
x2
6
+
y2
3
=1
得（1+2k2）x2-12k2x+18k2-6=0．
因为直线l与椭圆C交于不同的两点M，N，所以△=144k4-4（1+2k2）（18k2-6）=24（1-k2）＞0，解得-1＜k＜1．
设M，N的坐标分别为（x1，y1），（x2，y2），则x1+x2=
12k2
1+2k2
，x1x2=
18k2-6
1+2k2
，
y1=k（x1-3），y2=k（x2-3）．
所以
BM
•
BN
=(x1-3)(x2-3)+y1y2
=（1+k2）[x1x2-3（x1+x2）+9]=
3+3k2
1+2k2
=
3
2
+
3
2(1+2k2)
．
因为-1＜k＜1，所以2＜
3
2
+
3
2(1+2k2)
≤3．
故
BM
•
BN
的取值范围为（2，3]．
（Ⅲ）由（Ⅱ）得kAM+kAN=
y1-1
x1-2
+
y2-1
x2-2

=
(kx1-3k-1)(x2-2)+(kx2-3k-1)(x1-2)
(x1-2)(x2-2)
=
2kx1x2-(5k+1)(x1+x2)+12k+4
x1x2-2(x1+x2)+4

=
2k(18k2-6)-(5k+1)•12k2+(12k+4)(1+2k2)
18k2-6-24k2+4(1+2k2)
=
-4k2+4
2k2-2
=-2．
所以kAM+kAN为定值-2．
练习册系列答案
相关题目
如图，已知椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)过点(1，
2
2
)，离心率为
2
2
，左、右焦点分别为F1、F2．点P为直线l：x+y=2上且不在x轴上的任意一点，直线PF1和PF2与椭圆的交点分别为A、B和C、D，O为坐标原点．设直线PF1、PF2的斜率分别为k1、k2．
（Ⅰ）证明：
1
k1
-
3
k2
=2；
（Ⅱ）问直线l上是否存在点P，使得直线OA、OB、OC、OD的斜率kOA、kOB、kOC、kOD满足kOA+kOB+kOC+kOD=0？若存在，求出所有满足条件的点P的坐标；若不存在，说明理由．
过x轴上动点A（a，0）引抛物线y=x2+1的两条切线AP、AQ，P、Q为切点．
（1）若切线AP，AQ的斜率分别为k1和k2，求证：k1•k2为定值，并求出定值；
（2）求证：直线PQ恒过定点，并求出定点坐标；
（3）当
S△APO
PQ
最小时，求
AQ
•
AP
的值．
已知椭圆C1：
x2
4
+
y2
3
=1和抛物线C2：y2=2px（p＞0），过点M（1，0）且倾斜角为
π
3
的直线与抛物线交于A、B，与椭圆交于C、D，当|AB|：|CD|=5：3时，求p的值．
已知椭圆C的焦点为F1（-1，0）、F2（1，0），点P（-1，
2
2
）在椭圆上．
（1）求椭圆C的方程；
（2）若抛物线E：y2=2px（p＞0）与椭圆C相交于点M、N，当△OMN（O是坐标原点）的面积取得最大值时，求P的值．
（3）在（2）的条件下，过点F2作任意直线l与抛物线E相交于点A、B两点，则直线AF1与直线BF1的斜率之和是否为定值？若是，求出定值；若不是，说明理由．
已知点P(-1，
3
2
)是椭圆E：
x2
a2
+
y2
b2
=1（a＞b＞0）上一点，F1、F2分别是椭圆E的左、右焦点，O是坐标原点，PF1⊥x轴．
（1）求椭圆E的方程；
（2）设A、B是椭圆E上两个动点，是否存在λ，满足
PA
+
PB
=λ
PO
（0＜λ＜4，且λ≠2），且M（2，1）到AB的距离为
5
？若存在，求λ值；若不存在，说明理由．
在平面直角坐标系xOy中，△ABC的顶点B、C的坐标为B（-2，0），C（2，0），直线AB，AC的斜率乘积为-
1
4
，设顶点A的轨迹为曲线E．
（1）求曲线E的方程；
（2）设曲线E与y轴负半轴的交点为D，过点D作两条互相垂直的直线l1，l2，这两条直线与曲线E的另一个交点分别为M，N．设l1的斜率为k（k≠0），△DMN的面积为S，试求
S
|k|
的取值范围．
如图，将圆p：x2+y2=4上任意一点P′的纵坐标变为原来的一半（横坐标不变），得到点P，并设点P的轨迹为曲线C．
（1）求C的方程；
（2）设o为坐标原点，过点Q（
3
，0）的直线l与曲线C交于两点A，B，线段AB的中点为N，且
OE
=2
ON
，点E在曲线C上，求直线l：
x
a
+
y
b
=1的方程．
如图所示，设点F坐标为（1，0），点P在y轴上运动，点M在x轴运动上，其中
PM
•
PF
=0，若动点N满足条件
PN
=
MP

（Ⅰ）求动点N的轨迹E的方程；
（Ⅱ）过点F（1，0）的直线l和l′分别与曲线E交于A、B两点和C、D两点，若l⊥l′，试求四边形ACBD的面积的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网