题目内容
3.求和:1+2+4+8+16+…+29=1023.分析 利用等比数列的前n项和公式即可得出.
解答 解:数列{2n-1}是等比数列.首项为1,公比为2.
∴原式=$\frac{{2}^{10}-1}{2-1}$=1023.
故答案为:1023.
点评 本题考查了等比数列的前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
18.若m、n为两条不重合的直线,α、β为两个不重合的平面,则下列命题正确的是( )
| A. | 若m、n都平行于平面α,则m、n一定不是相交直线. | |
| B. | m、n在平面α内的射影互相垂直,则m、n互相垂直 | |
| C. | 若m、n都垂直于平面α,则m、n一定是平行直线. | |
| D. | 已知α、β互相垂直,m、n互相垂直,若m⊥α,则n⊥β |
8.已知:X~N(μ,δ2),且EX=5,DX=4,则P(3<x≤7)≈( )
| A. | 0.045 6 | B. | 0.50 | C. | 0.682 6 | D. | 0.9544 |
12.如图所示,程序执行后的输出结果为( )
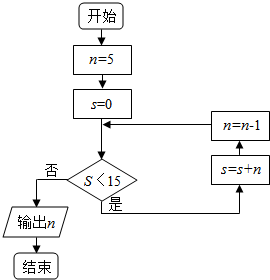

| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
13.已知实数x,y满足不等式组$\left\{{\begin{array}{l}{2x-y+2≥0}\\{x+y-2≥0}\\{x≤2}\end{array}}\right.$,则$\frac{y-1}{x+3}$的取值范围是( )
| A. | $(-∞,-\frac{1}{5}]∪[1,+∞)$ | B. | $[\frac{1}{3},1]$ | C. | [-$\frac{1}{5}$,$\frac{1}{3}$] | D. | [-$\frac{1}{5}$,1] |