题目内容
已知向量
，
，且函数
.
（Ⅰ）当函数
在
上的最大值为3时，求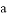
的值；
（Ⅱ）在（Ⅰ）的条件下，若对任意的
，函数
，
的图像与直线
有且仅有两个不同的交点，试确定
的值.并求函数在
上的单调递减区间.
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
小学生10分钟口算测试100分系列答案题目内容
已知向量，，且函数.
（Ⅰ）当函数在上的最大值为3时，求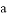的值；
（Ⅱ）在（Ⅰ）的条件下，若对任意的，函数，的图像与直线有且仅有两个不同的交点，试确定的值.并求函数在上的单调递减区间.
小学生10分钟口算测试100分系列答案
中，侧面
是边长为2的菱形，且
.点
在平面
，且
上，
，点
在线段
上，且
.
平面
；
的体积.
，
，
的最小值为
．
的值；
，
，且
．求证：
．
的参数方程
（
为参数）．以坐标原点
为极点，
轴的正半轴为极轴，建立极坐标系，两种坐标系中取相同的单位长度，曲线
的极坐标方程为
．
，且
，求直线的倾斜角
的值.
的导函数为
，且当
时，
，若
，则
的解集为（ ）
B. 
D. 
，我们把使乘积
…
为整数的数
叫做“优数”，则在区间（1,2004）内的所有优数的和为 （ ）
，则函数
的图象大致为（ ）
B. 
D. 
，则函数
在
的值域是__________．