题目内容
根据市场调查结果，预测某种家用商品从年初开始的n个月内累积的需求量Sn(万件)近似地满足关系式Sn＝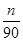
(21n－n2－5)(n＝1，2，…，12)，按此预测，在本年度内，需求量超过1.5万件的月份是________．
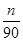(21n－n2－5)(n＝1，2，…，12)，按此预测，在本年度内，需求量超过1.5万件的月份是________．7、8
由Sn解出an＝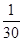
(－n2＋15n－9)，再解不等式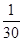(－n2＋15n－9)>1.5，得6<n<9.
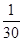(－n2＋15n－9)，再解不等式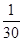(－n2＋15n－9)>1.5，得6<n<9.
练习册系列答案
相关题目
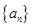为等差数列，且
.
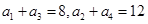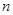项和为
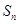，若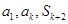
成等比数列，求正整数
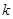的值.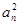
}成等差数列.
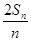＝an＋1－
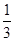n2－n－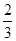
，n∈N*.
.
，
，
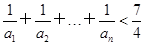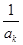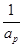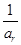成等差数列？若存在，用k分别表示p和r(只要写出一组)；若不存在，请说明理由．
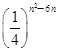(n∈N*)，bn＝log2an，则数列{bn}的前n项和Sn取最大时，n＝________．
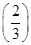n}中的最大项是第k项,则k= .