题目内容
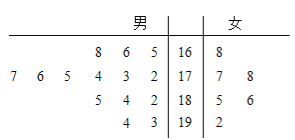
【题目】![]() 公司从某大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分),公司规定:成绩在180分以上者到“甲部门”工作;180分以下者到“乙部门”工作.
公司从某大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分),公司规定:成绩在180分以上者到“甲部门”工作;180分以下者到“乙部门”工作.
(1)求男生成绩的中位数及女生成绩的平均值;
(2)如果用分层抽样的方法从“甲部门”人选和“乙部门”人选中共选取5人,再从这5人中选2人,那么至少有一人是“甲部门”人选的概率是多少?
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)根据中位数、平均数的概念写出中位数、平均数;(2)利用分层抽样及列举法、古典概型公式即可得出.
试题解析:
(1)男生有14人,中间两个成绩是175和176,它们的平均数为175.5,
因此男生的成绩的中位数为175.5,
女生的平均成绩![]() .
.
(2)用分层抽样的方法从“甲部门”和“乙部门”20人中抽取5人,每个人被抽到的概率是![]() .
.
根据茎叶图,“甲部门”人选有8人,“乙部门”人选有12人.
所以选中的“甲部门”人选有![]() 人,“乙部门”人选有
人,“乙部门”人选有![]() 人.
人.
记选中的“甲部门”的人员为![]() ,
,![]() ,选中的“乙部门”人员为
,选中的“乙部门”人员为![]() ,
,![]() ,
,![]() ,从这5人中选2人的所有可能情况为:
,从这5人中选2人的所有可能情况为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共10种,
共10种,
其中至少有1人是“甲部门”人选的结果有7种,
因此,至少有1人是“甲部门”人选的概率是![]() .
.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目