题目内容
已知下列四个命题:
①若函数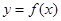 在
在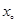 处的导数
处的导数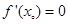 ,则它在
,则它在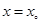 处有极值;
处有极值;
②若不论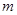 为何值,直线
为何值,直线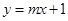 均与曲线
均与曲线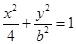 有公共点,则
有公共点,则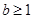 ;
;
③若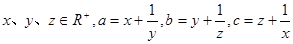 ,则
,则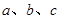 中至少有一个不小于2;
中至少有一个不小于2;
④若命题“存在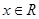 ,使得
,使得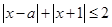 ”是假命题,则
”是假命题,则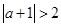 ;
;
以上四个命题正确的是 (填入相应序号).
①若函数
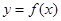 在
在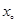 处的导数
处的导数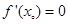 ,则它在
,则它在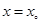 处有极值;
处有极值;②若不论
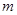 为何值,直线
为何值,直线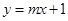 均与曲线
均与曲线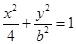 有公共点,则
有公共点,则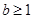 ;
;③若
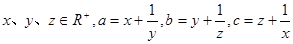 ,则
,则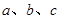 中至少有一个不小于2;
中至少有一个不小于2;④若命题“存在
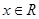 ,使得
,使得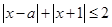 ”是假命题,则
”是假命题,则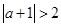 ;
;以上四个命题正确的是 (填入相应序号).
③④
解:因为
①若函数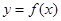 在
在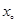 处的导数
处的导数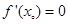 ,则它在
,则它在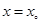 处有极值;不一定,比如三次函数在x=0处。
处有极值;不一定,比如三次函数在x=0处。
②若不论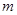 为何值,直线
为何值,直线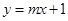 均与曲线
均与曲线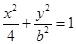 有公共点,则
有公共点,则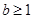 ;联立方程组,则方程恒有解,则得到b的范围,
;联立方程组,则方程恒有解,则得到b的范围,
③若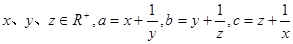 ,则
,则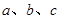 中至少有一个不小于2;成立根据均值不等式得到。
中至少有一个不小于2;成立根据均值不等式得到。
④若命题“存在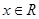 ,使得
,使得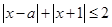 ”是假命题,则
”是假命题,则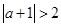 ;利用否定得到a的范围
;利用否定得到a的范围
①若函数
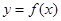 在
在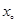 处的导数
处的导数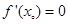 ,则它在
,则它在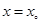 处有极值;不一定,比如三次函数在x=0处。
处有极值;不一定,比如三次函数在x=0处。②若不论
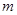 为何值,直线
为何值,直线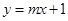 均与曲线
均与曲线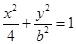 有公共点,则
有公共点,则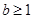 ;联立方程组,则方程恒有解,则得到b的范围,
;联立方程组,则方程恒有解,则得到b的范围,③若
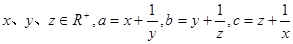 ,则
,则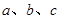 中至少有一个不小于2;成立根据均值不等式得到。
中至少有一个不小于2;成立根据均值不等式得到。④若命题“存在
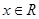 ,使得
,使得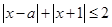 ”是假命题,则
”是假命题,则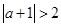 ;利用否定得到a的范围
;利用否定得到a的范围
练习册系列答案
相关题目
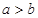 ,则
,则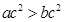 ;(2)直线
;(2)直线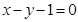 的倾斜角为
的倾斜角为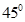 ,纵截
,纵截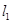 :
: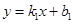 与直线
与直线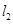 :
: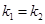 且
且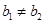 ;
;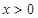 且
且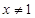 时,
时,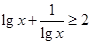 ;(5)到坐标轴距离相等的点的轨迹方程为
;(5)到坐标轴距离相等的点的轨迹方程为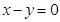 ; 其中真命题的个数是
; 其中真命题的个数是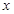 ,使
,使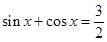 ;②若
;②若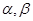 是第一象限角,且
是第一象限角,且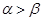 ,则
,则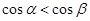 ;
;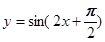 是偶函数; ④函数
是偶函数; ④函数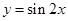 的图象向左平移
的图象向左平移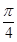 个单位,得到函
个单位,得到函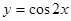 的图象.
的图象.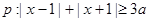 恒成立,命题
恒成立,命题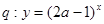 为减函数,若
为减函数,若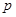 且
且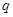 为真命题,则
为真命题,则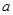 的取值范围是 .
的取值范围是 .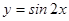 的单调增区间是[
的单调增区间是[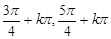 ],(k∈Z)② 函数
],(k∈Z)② 函数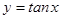 在
在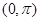 内是增函数③若数列
内是增函数③若数列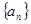 满足
满足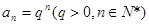 ,则
,则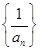 是等比数列;④若数列
是等比数列;④若数列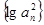 是等差数列; ⑤函数
是等差数列; ⑤函数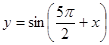 是偶函数,其中正确的命题序号是
是偶函数,其中正确的命题序号是 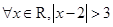 ”的否定是_____________________________ .
”的否定是_____________________________ . 中,顶点
中,顶点 到对角线
到对角线 和到平面
和到平面 的距离分别为
的距离分别为 和
和 ,则下列命题中正确的是( )
,则下列命题中正确的是( ) 的取值范围为
的取值范围为

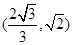

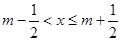 (其中m为整数),则m叫做离实数x最近的整数,记作{x},即
(其中m为整数),则m叫做离实数x最近的整数,记作{x},即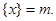 在此基础上给出下列关于函数
在此基础上给出下列关于函数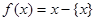 的四个命题:
的四个命题: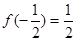 ;②
;②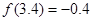 ;③
;③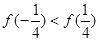 ;④
;④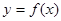 的定义域是R,
的定义域是R,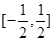 . 则其中真命题的序号是 ( )
. 则其中真命题的序号是 ( )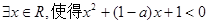 ”是真命题,则实数
”是真命题,则实数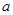 的取值范围是
的取值范围是