题目内容
【题目】已知圆![]() 经过
经过![]() 两点,且圆心在直线
两点,且圆心在直线![]() 上.
上.
(Ⅰ)求圆![]() 的标准方程;
的标准方程;
(Ⅱ)设直线![]() 经过点
经过点![]() ,且
,且![]() 与圆
与圆![]() 相交所得弦长为
相交所得弦长为![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() 或
或![]() .
.
【解析】
试题分析:(Ⅰ)求圆的方程,需要三个独立条件,一般设标准式,代入三个条件,解方程组即可;本题也可设成圆的一般式![]() ,再将两个点坐标代入,解方程组可得.(Ⅱ)涉及圆中弦长问题,一般利用垂径定理,即将弦长条件转化为圆心到直线距离,再根据点到直线距离公式求直线斜率,注意验证直线斜率不存在的情形.
,再将两个点坐标代入,解方程组可得.(Ⅱ)涉及圆中弦长问题,一般利用垂径定理,即将弦长条件转化为圆心到直线距离,再根据点到直线距离公式求直线斜率,注意验证直线斜率不存在的情形.
试题解析:解:(Ⅰ)设圆![]() 的圆心坐标为
的圆心坐标为![]() ,
,
依题意,有![]() ,
,
解得![]() ,所以
,所以![]() ,
,
所以圆![]() 的标准方程为
的标准方程为![]() .
.
(Ⅱ)依题意,圆![]() 的圆心
的圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
(1)若直线![]() 的斜率不存在,则
的斜率不存在,则![]() ,符合题意,此时直线的方程为
,符合题意,此时直线的方程为![]() .
.
(2)若直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为
的方程为![]() ,即
,即![]() ,则
,则![]() ,解得
,解得![]() .
.
此时直线![]() 的方程为
的方程为![]()
综上,直线![]() 的方程为
的方程为![]() 或
或![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
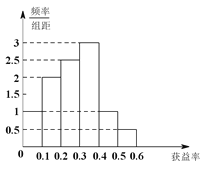
【题目】某中学从高三男生中随机抽取100名学生,将他们的身高数据进行整理,得到下侧的频率分布表.
组号 | 分组 | 频率 |
第1组 | [160,165) | 0.05 |
第2组 |
| 0.35 |
第3组 |
| 0.3 |
第4组 |
| 0.2 |
第5组 |
| 0.1 |
合计 | 1.00 | |
(Ⅰ)为了能对学生的体能做进一步了解,该校决定在第3,4,5组中用分层抽样的方法抽取6名学生进行体能测试,问第3,4,5组每组各应抽取多少名学生进行测试;
(Ⅱ)在(Ⅰ)的前提下,学校决定在6名学生中随机抽取2名学生进行引体向上测试,求第3组中至少有一名学生被抽中的概率;
(Ⅲ)试估计该中学高三年级男生身高的中位数位于第几组中,并说明理由.