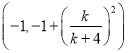题目内容
【题目】在等比数列![]() 中,已知
中,已知![]() ,
,![]() .设数列
.设数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]() ,
,![]() (
(![]() ,
,![]() ).
).
(1)求数列![]() 的通项公式;
的通项公式;
(2)证明:数列![]() 是等差数列;
是等差数列;
(3)是否存在等差数列![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() ?若存在,求出所有符合题意的等差数列
?若存在,求出所有符合题意的等差数列![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
【答案】(1)![]() (2)见解析(3)存在唯一的等差数列
(2)见解析(3)存在唯一的等差数列![]() ,其通项公式为
,其通项公式为![]() ,
,![]() 满足题设
满足题设
【解析】
(1)由![]() ,
,![]() 可得公比
可得公比![]() ,即得;(2)由(1)和
,即得;(2)由(1)和![]() 可得数列
可得数列![]() 的递推公式,即可知
的递推公式,即可知![]() 结果为常数,即得证;(3)由(2)可得数列
结果为常数,即得证;(3)由(2)可得数列![]() 的通项公式,
的通项公式,![]() ,设出等差数列
,设出等差数列![]() ,再根据不等关系
,再根据不等关系![]() 来算出
来算出![]() 的首项和公差即可.
的首项和公差即可.
(1)设等比数列![]() 的公比为q,因为
的公比为q,因为![]() ,
,![]() ,所以
,所以![]() ,解得
,解得![]() .
.
所以数列![]() 的通项公式为:
的通项公式为:![]() .
.
(2)由(1)得,当![]() ,
,![]() 时,可得
时,可得![]() ①,
①,
![]() ②
②
②![]() ①得,
①得,![]() ,
,
则有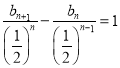 ,即
,即![]() ,
,![]() ,
,![]() .
.
因为![]() ,由①得,
,由①得,![]() ,所以
,所以![]() ,
,
所以![]() ,
,![]() .
.
所以数列![]() 是以
是以![]() 为首项,1为公差的等差数列.
为首项,1为公差的等差数列.
(3)由(2)得![]() ,所以
,所以![]() ,
,![]()
![]() .
.
假设存在等差数列![]() ,其通项
,其通项![]() ,
,
使得对任意![]() ,都有
,都有![]() ,
,
即对任意![]() ,都有
,都有![]() .③
.③
首先证明满足③的![]() .若不然,
.若不然,![]() ,则
,则![]() ,或
,或![]() .
.
(i)若![]() ,则当
,则当![]() ,
,![]() 时,
时,![]() ,
,
这与![]() 矛盾.
矛盾.
(ii)若![]() ,则当
,则当![]() ,
,![]() 时,
时,![]() .
.
而![]() ,
,![]() ,所以
,所以![]() .
.
故![]() ,这与
,这与![]() 矛盾.所以
矛盾.所以![]() .
.
其次证明:当![]() 时,
时,![]() .
.
因为![]() ,所以
,所以![]() 在
在![]() 上单调递增,
上单调递增,
所以,当![]() 时,
时,![]() .
.
所以当![]() ,
,![]() 时,
时,![]() .
.
再次证明![]() .
.
(iii)若![]() 时,则当
时,则当![]() ,
,![]() ,
,![]() ,
,![]() ,这与③矛盾.
,这与③矛盾.
(iv)若![]() 时,同(i)可得矛盾.所以
时,同(i)可得矛盾.所以![]() .
.
当![]() 时,因为
时,因为![]() ,
,![]() ,
,
所以对任意![]() ,都有
,都有![]() .所以
.所以![]() ,
,![]() .
.
综上,存在唯一的等差数列![]() ,其通项公式为
,其通项公式为![]() ,
,![]() 满足题设.
满足题设.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目