题目内容
【题目】已知直线![]() 是曲线
是曲线![]() 的切线.
的切线.
(1)求函数![]() 的解析式,
的解析式,
(2)若![]() ,证明:对于任意
,证明:对于任意![]() ,
,![]() 有且仅有一个零点.
有且仅有一个零点.
【答案】(1)![]() (2)证明见解析
(2)证明见解析
【解析】
(1)对函数求导,并设切点![]() ,利用点既在曲线上、又在切线上,列出方程组,解得
,利用点既在曲线上、又在切线上,列出方程组,解得![]() ,即可得答案;
,即可得答案;
(2)当x充分小时![]() ,当x充分大时
,当x充分大时![]() ,可得
,可得![]() 至少有一个零点. 再证明零点的唯一性,即对函数求导得
至少有一个零点. 再证明零点的唯一性,即对函数求导得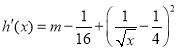 ,对
,对![]() 分
分![]() 和
和![]() 两种情况讨论,即可得答案.
两种情况讨论,即可得答案.
(1)根据题意,![]() ,设直线
,设直线![]() 与曲线
与曲线![]() 相切于点
相切于点![]() .
.
根据题意,可得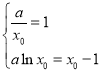 ,解之得
,解之得![]() ,
,
所以![]() .
.
(2)由(1)可知![]() ,
,
则当x充分小时![]() ,当x充分大时
,当x充分大时![]() ,∴
,∴![]() 至少有一个零点.
至少有一个零点.
∵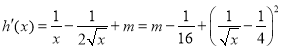 ,
,
①若![]() ,则
,则![]() ,
,![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]() 有唯一零点.
有唯一零点.
②若![]() 令
令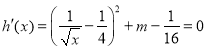 ,得
,得![]() 有两个极值点,
有两个极值点,
∵![]() ,∴
,∴![]() ,∴
,∴![]() .
.
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
∴极大值为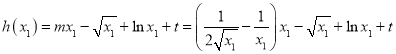 .
.![]() ,又
,又 ,
,
∴![]() 在(0,16)上单调递增,
在(0,16)上单调递增,
∴![]() ,
,
∴![]() 有唯一零点.
有唯一零点.
综上可知,对于任意![]() ,
,![]() 有且仅有一个零点.
有且仅有一个零点.

【题目】某公司欲对员工饮食习惯进行一次调查,从某科室的100人中的饮食结构调查结果统计如下表.
主食蔬菜 | 主食肉类 | 总计 | |
不超过45岁 | 15 | 40 | |
45岁以上 | 20 | ||
总计 |
(1)完成![]() 列联表,并判断能否有99%的把握认为员工的饮食习惯与年龄有关?
列联表,并判断能否有99%的把握认为员工的饮食习惯与年龄有关?
(2)在45岁以上员工中按照饮食习惯进行分层抽样抽出一个容量为6的样本,从这6个人中随机抽取3个人,求这3个人都主食蔬菜的概率.
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
 .
.
【题目】某同学用“随机模拟方法”计算曲线![]() 与直线
与直线![]() 所围成的曲边三角形的面积时,用计算机分别产生了10个在区间[1,e]上的均匀随机数xi和10个在区间[0,1]上的均匀随机数
所围成的曲边三角形的面积时,用计算机分别产生了10个在区间[1,e]上的均匀随机数xi和10个在区间[0,1]上的均匀随机数![]()
![]() ,其数据如下表的前两行.
,其数据如下表的前两行.
x | 2.50 | 1.01 | 1.90 | 1.22 | 2.52 | 2.17 | 1.89 | 1.96 | 1.36 | 2.22 |
y | 0.84 | 0.25 | 0.98 | 0.15 | 0.01 | 0.60 | 0.59 | 0.88 | 0.84 | 0.10 |
lnx | 0.90 | 0.01 | 0.64 | 0.20 | 0.92 | 0.77 | 0.64 | 0.67 | 0.31 | 0.80 |
由此可得这个曲边三角形面积的一个近似值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()