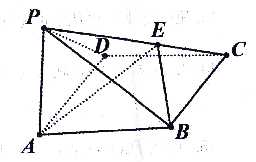
题目内容
【题目】已知平面向量![]() ,满足
,满足![]() 且
且![]() ,若对每一个确定的向量
,若对每一个确定的向量![]() ,记
,记![]() 的最小值为
的最小值为![]() ,则当
,则当![]() 变化时,
变化时,![]() 的最大值为( )
的最大值为( )
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
【答案】B
【解析】
根据题意,建立平面直角坐标系.令![]()
![]() .
.![]() 为
为![]() 中点.由
中点.由![]() 即可求得
即可求得![]() 点的轨迹方程.将
点的轨迹方程.将![]() 变形,结合
变形,结合![]() 及平面向量基本定理可知
及平面向量基本定理可知![]() 三点共线.由圆切线的性质可知
三点共线.由圆切线的性质可知![]() 的最小值
的最小值![]() 即为
即为![]() 到直线
到直线![]() 的距离最小值,且当
的距离最小值,且当![]() 与圆
与圆![]() 相切时,
相切时,![]() 有最大值.利用圆的切线性质及点到直线距离公式即可求得直线方程,进而求得原点到直线的距离,即为
有最大值.利用圆的切线性质及点到直线距离公式即可求得直线方程,进而求得原点到直线的距离,即为![]() 的最大值.
的最大值.
根据题意,![]() 设
设![]() ,
,![]()
则![]()
由![]() 代入可得
代入可得![]()
即![]() 点的轨迹方程为
点的轨迹方程为![]()
又因为![]() ,变形可得
,变形可得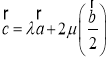 ,即
,即![]() ,且
,且![]()
所以由平面向量基本定理可知![]() 三点共线,如下图所示:
三点共线,如下图所示:
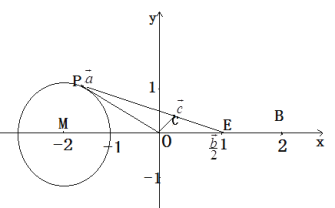
所以![]() 的最小值
的最小值![]() 即为
即为![]() 到直线
到直线![]() 的距离最小值
的距离最小值
根据圆的切线性质可知,当![]() 与圆
与圆![]() 相切时,
相切时,![]() 有最大值
有最大值
设切线![]() 的方程为
的方程为![]() ,化简可得
,化简可得![]()
由切线性质及点![]() 到直线距离公式可得
到直线距离公式可得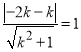 ,化简可得
,化简可得![]()
即![]()
所以切线方程为![]() 或
或![]()
所以当![]() 变化时,
变化时, ![]() 到直线
到直线![]() 的最大值为
的最大值为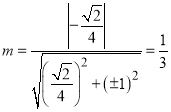
即![]() 的最大值为
的最大值为![]()
故选:B

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目