题目内容
13．若f（x）=$\frac{1}{2}$x2-ax+alnx在（0，+∞）上单调增，则实数a的取值范围为（ ）| A． | （0，+∞） | B． | （-∞，4] | C． | [0，4] | D． | （4，+∞） |
分析 由题意求导可得f′（x）=x-a+$\frac{a}{x}$=$\frac{{x}^{2}-ax+a}{x}$≥0恒成立；从而讨论确定恒成立的条件即可．
解答 解：∵f（x）=$\frac{1}{2}$x2-ax+alnx在（0，+∞）上单调增，
∴f′（x）=x-a+$\frac{a}{x}$=$\frac{{x}^{2}-ax+a}{x}$≥0恒成立；
当a＜0时，显然不可能恒成立；
当a=0时，显然恒成立；
当a＞0时，△=a2-4a≤0，
故a≤4；
综上所述，实数a的取值范围为[0，4]；
故选：C．
点评 本题考查了导数的综合应用及恒成立问题的应用．
练习册系列答案
相关题目
3．已知平面内A，B两点的坐标分别为（2，2），（0，-2），O为坐标原点，动点P满足|$\overrightarrow{BP}$|=1，则|$\overrightarrow{OA}$+$\overrightarrow{OP}$|的取值范围为（ ）
| A． | （1，3） | B． | [1，3] | C． | （1，9） | D． | [1，9] |
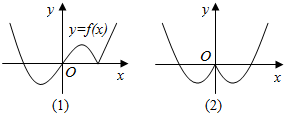已知如图（1）的图象对应的函数为y=f（x），给出①y=f（|x|）；②y=|f（x）|-a；③y=-f（|x|）；④y=f（-|x|）．⑤y=|f（|x|）|-a，则如图（2）的图象对应的函数可能是五个式子中的（ ）
某校从参加高一年级期末考试的学生中抽出40名学生，将其成绩（均为整数）分成六段[40，50），[50，60）…[90，100]后画出如下部分频率分布直方图，观察图形的信息，回答下列问题：